题目内容
(本小题满分14分)已知函数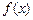 满足
满足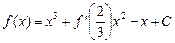 (其中
(其中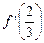 为
为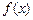 在点
在点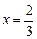 处的导数,
处的导数,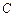 为常数).(1)求函数
为常数).(1)求函数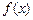 的单调区间;(2)若方程
的单调区间;(2)若方程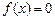 有且只有两个不等的实数根,求常数
有且只有两个不等的实数根,求常数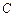 ;(3)在(2)的条件下,若
;(3)在(2)的条件下,若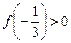 ,求函数
,求函数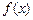 的图象与
的图象与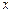 轴围成的封闭图形的面积.
轴围成的封闭图形的面积.
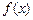 满足
满足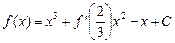 (其中
(其中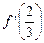 为
为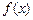 在点
在点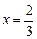 处的导数,
处的导数,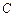 为常数).(1)求函数
为常数).(1)求函数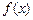 的单调区间;(2)若方程
的单调区间;(2)若方程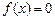 有且只有两个不等的实数根,求常数
有且只有两个不等的实数根,求常数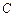 ;(3)在(2)的条件下,若
;(3)在(2)的条件下,若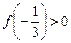 ,求函数
,求函数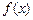 的图象与
的图象与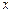 轴围成的封闭图形的面积.
轴围成的封闭图形的面积.(Ⅰ)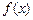 的单调递增区间是
的单调递增区间是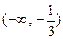 和
和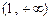 ;
;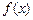 的单调递减区间是
的单调递减区间是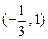 . (Ⅱ)
. (Ⅱ) 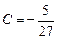 或
或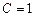 (Ⅲ)
(Ⅲ)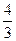
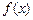 的单调递增区间是
的单调递增区间是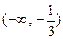 和
和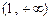 ;
;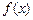 的单调递减区间是
的单调递减区间是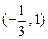 . (Ⅱ)
. (Ⅱ) 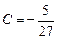 或
或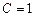 (Ⅲ)
(Ⅲ)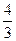
:(1)由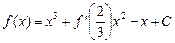 ,得
,得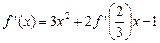 .
.
取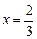 ,得
,得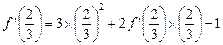 ,解之,得
,解之,得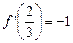 ,
,
∴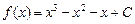 .…2分从而
.…2分从而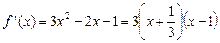 ,
,
列表如下:
∴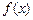 的单调递增区间是
的单调递增区间是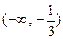 和
和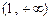 ;
;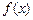 的单调递减区间是
的单调递减区间是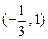 .4分
.4分
(2)由(1)知,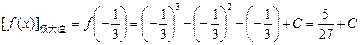 ;
;
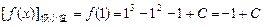 .………………………………6分
.………………………………6分
∴方程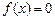 有且只有两个不等的实数根,等价于
有且只有两个不等的实数根,等价于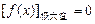 或
或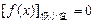 .………8分∴常数
.………8分∴常数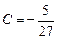 或
或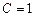 .………9分
.………9分
(3)由(2)知,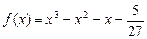 或
或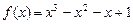 .
.
而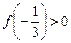 ,所以
,所以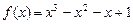 .………10分
.………10分
令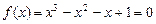 ,得
,得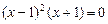 ,
,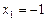 ,
,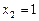 .………12分
.………12分
∴所求封闭图形的面积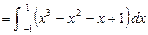
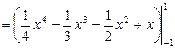
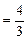 .14分
.14分
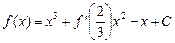 ,得
,得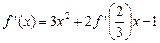 .
.取
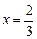 ,得
,得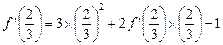 ,解之,得
,解之,得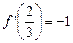 ,
,∴
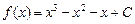 .…2分从而
.…2分从而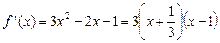 ,
,列表如下:
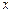 | 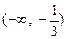 | 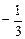 | 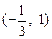 | 1 | 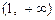 |
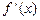 | + | 0 | - | 0 | + |
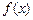 | ↗ | 有极大值 | ↘ | 有极小值 | ↗ |
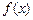 的单调递增区间是
的单调递增区间是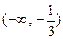 和
和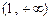 ;
;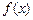 的单调递减区间是
的单调递减区间是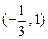 .4分
.4分(2)由(1)知,
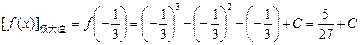 ;
;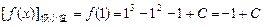 .………………………………6分
.………………………………6分∴方程
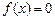 有且只有两个不等的实数根,等价于
有且只有两个不等的实数根,等价于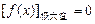 或
或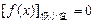 .………8分∴常数
.………8分∴常数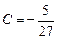 或
或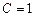 .………9分
.………9分(3)由(2)知,
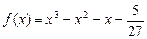 或
或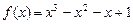 .
.而
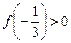 ,所以
,所以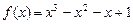 .………10分
.………10分令
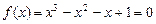 ,得
,得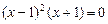 ,
,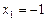 ,
,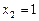 .………12分
.………12分∴所求封闭图形的面积
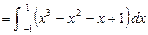
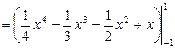
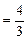 .14分
.14分
练习册系列答案
相关题目
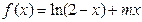 在区间
在区间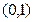 上是增函数.(1)求实数m的取值范围;(2)若数列
上是增函数.(1)求实数m的取值范围;(2)若数列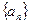 满足
满足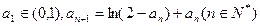 ,证明:
,证明: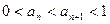 .
. 上求一点P,当△PAB面积最大时,P点坐标为 .
上求一点P,当△PAB面积最大时,P点坐标为 .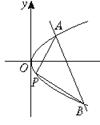
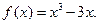 (Ⅰ)求曲线
(Ⅰ)求曲线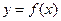 在点
在点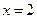 处的切线方程;
处的切线方程;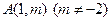 可作曲线
可作曲线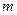 的取值范围.
的取值范围.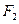 为圆心,过另一焦点
为圆心,过另一焦点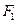 的圆被右准线截的两段弧长之比2:1,
的圆被右准线截的两段弧长之比2:1,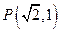 为此平面上一定点,且
为此平面上一定点,且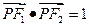 .(1)求椭圆的方程(2)若直线
.(1)求椭圆的方程(2)若直线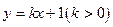 与椭圆交于如图两点A、B,令
与椭圆交于如图两点A、B,令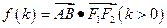 。求函数
。求函数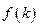 的值域
的值域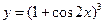 的导数
的导数 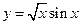 导数为( )
导数为( )


