题目内容

平面四边形ABCD中，AB= $数学公式$ ，AD=DC=CB=1，△ABD和△BCD的面积分别为S，T，则S²+T²的最大值是________．

$\text{[math]}$
分析：先利用余弦定理求出cosA和cosC的关系，再用含角A，C的面积公式求出S²+T²，进而转化为cosA的二次函数，即可求出最大值．
解答：

解：由题意， $\text{[math]}$
∵ $\text{[math]}$
∴ $\text{[math]}$
∴S²+T²= $\text{[math]}$ = $\text{[math]}$
= $\text{[math]}$ = $\text{[math]}$
∴ $\text{[math]}$ 时，S²+T²的最大值是 $\text{[math]}$
故答案为： $\text{[math]}$
点评：本题以平面四边形为载体，考查余弦定理的运用，考查三角函数，解题的关键是转化为cosA的二次函数．

练习册系列答案

快乐天天练暑假作业安徽师范大学出版社系列答案

欢乐岛暑假小小练系列答案

过好暑假每一天系列答案

暑假生活学习与生活系列答案

小学升初中衔接教材中南大学出版社系列答案

暑假衔接起跑线系列答案

暑假直通车系列答案

快乐暑假甘肃少年儿童出版社系列答案

学习总动员暑假总复习系列答案

暑假一本通内蒙古大学出版社系列答案

相关题目

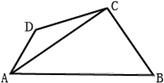如图，平面四边形ABCD中，AB=13，三角形ABC的面积为S_△ABC=25，cos∠DAC=

=120，
求：（1）AC的长；（2）cos∠BAD．

如图 I，平面四边形ABCD中，∠A=60°，∠ABC=150°，AB=AD=2BC=4，把△ABD沿直线BD折起，使得平面ABD⊥平面BCD，连接AC得到如图 II所示四面体A-BCD．设点O，E，F分别是BD，AB，AC的中点．连接CE，BF交于点G，连接OG．
（1）证明：OG⊥AC；
（2）求二面角B-AD-C的大小．

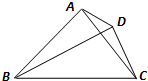如图，在平面四边形ABCD中，若AB=2，CD=1，则(

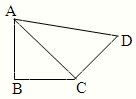如图，在平面四边形ABCD中，AB=BC=CD=a，∠ABC=90°，∠BCD=135°，沿对角线AC将此四边形折成直二面角．
（1）求证：AB⊥平面BCD
（2）求三棱锥D-ABC的体积
（3）求点C到平面ABD的距离．

如图甲，在平面四边形ABCD中，已知∠A=45°，∠C=90°，AB=BD=2CD，现将四边形ABCD沿BD折起，使平面ABD⊥平面BDC（如图乙），设点E为棱AD的中点．
（1）求证：DC⊥平面ABC；
（2）求BE与平面ABC所成角的正弦值大小．