题目内容
将边长为a的正方形ABCD沿对角线AC折起，使得BD=a，则三棱锥D-ABC的体积为
- A.
- B.
- C.
- D.
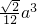
D
分析：取AC的中点O，连接DO，BO，求出三角形DOB的面积，求出AC 的长，即可求三棱锥D-ABC的体积．
解答：O是AC中点，连接DO，BO△ADC，△ABC都是等腰直角三角形 DO=B0=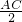
=
，BD=a△BDO也是等腰直角三角形 DO⊥AC，DO⊥BO DO⊥平面ABC DO就是三棱锥D-ABC的高 S△ABC=
a2三棱锥D-ABC的体积：
故选D．
点评：本题考查棱锥的体积，是基础题．
分析：取AC的中点O，连接DO，BO，求出三角形DOB的面积，求出AC 的长，即可求三棱锥D-ABC的体积．
解答：O是AC中点，连接DO，BO△ADC，△ABC都是等腰直角三角形 DO=B0=
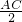=，BD=a△BDO也是等腰直角三角形 DO⊥AC，DO⊥BO DO⊥平面ABC DO就是三棱锥D-ABC的高 S△ABC=a2三棱锥D-ABC的体积：故选D．点评：本题考查棱锥的体积，是基础题．
练习册系列答案
相关题目
将边长为a的正方形ABCD沿对角线AC折起，使得BD=a，则三棱锥D-ABC的体积为（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
如图，将边长为a的正方形剪去阴影部分后，围成一个正三棱锥，则正三棱锥的体积是
如图，将边长为3的正方形ABCD绕中心O顺时针旋转α （0＜α＜