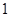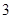题目内容
“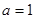 ”是“函数
”是“函数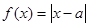 在区间
在区间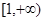 上为增函数”的( )
上为增函数”的( )
| A.充要条件 | B.必要不充分条件 |
| C.充分不必要条件 | D.既不充分也不必要条件 |
C
解析试题分析:显然,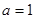 时,函数
时,函数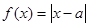 在区间
在区间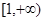 上为增函数。但反之,函数
上为增函数。但反之,函数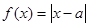 在区间
在区间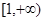 上为增函数时,不一定有
上为增函数时,不一定有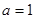 ,如
,如 时也可以,故“
时也可以,故“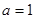 ”是“函数
”是“函数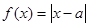 在区间
在区间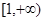 上为增函数”的充分不必要条件,选A。
上为增函数”的充分不必要条件,选A。
考点:充要条件的概念。
点评:简单题,涉及充要条件的判断问题,往往综合性较强,常用方法有:定义法、等价转化法、集合关系法。

练习册系列答案
 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
下列命题中的假命题是( )
A. | B. |
C. | D. |
下列命题为真命题的是
A.若 为真命题,则 为真命题,则 为真命题 为真命题 |
B.“ ”是“ ”是“ ”的充分不必要条件 ”的充分不必要条件 |
C.命题“若 ,则 ,则 ”的否命题为:“若 ”的否命题为:“若 ,则 ,则 ” ” |
D.命题p: , , ,则 ,则 : : , , |
 为方程
为方程 的解是
的解是 为函数f(x)极值点的 ( )
为函数f(x)极值点的 ( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
下列命题中,是真命题的是 ( )
A.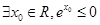 | B.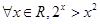 |
C.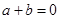 的充要条件是 的充要条件是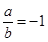 | D.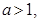 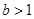 是 是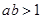 的充分条件 的充分条件 |
若集合 ,
, ,则“
,则“ ”是“
”是“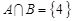 ”的 ( )
”的 ( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充分必要条件 | D.既不充分也不必要条件 |
命题“若 则
则 ”及其逆命题,否命题,逆否命题中真命题的个数可能是( )
”及其逆命题,否命题,逆否命题中真命题的个数可能是( )
| A.1 | B.2 | C.3 | D.都有可能 |
 :函数
:函数 恒过(1,2)点;命题
恒过(1,2)点;命题 :若函数
:若函数 为偶函数,则
为偶函数,则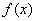 的图像关于直线
的图像关于直线 对称,则下列命题为真命题的是
对称,则下列命题为真命题的是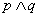



 ,且
,且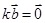 ,则
,则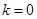 或
或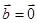 ,
,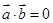 ,则
,则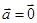 或
或 ,满足
,满足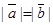 ,则
,则
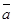 与
与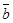 平行,则
平行,则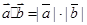 其中真命题的个数是( )
其中真命题的个数是( )