题目内容
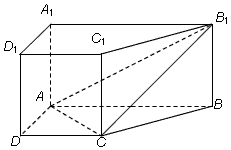
如图所示,直棱柱ABCD-A1B1C1D1中,底面ABCD是直角梯形,∠BAD=∠ADC=90°,AB=2AD=2CD=2.

(1)求证:AC⊥平面BB1C1C;
(2)在A1B1上是否存一点P,使得DP与平面ACB1平行?证明你的结论.
答案:
解析:
解析:
|
(1)证明:直棱柱ABCD-A1B1C1D1中,BB1⊥平面ABCD,∴BB1⊥AC;2分 又∵∠BAD=∠ADC=90°,AB=2AD=2CD=2 ∴AC= 又BB1∩BC=B;∴AC⊥平面BB1C1C.6分 (2)存在点P,P为A1B1的中点可满足要求.7分 证明:由P为A1B1的中点,有PB1∥AB,且PB1= 又∵CD∥AB,CD= ∴CDPB1为平行四边形,∴DP∥CB1;10分 又CB1 |

练习册系列答案
相关题目
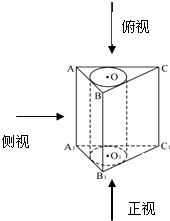 如图所示,直三棱柱ABC-A1B1C1的侧棱AA1=6,底面三角形的边AB=3,BC=4,AC=5.以上、下底的内切圆为底面,挖去一个圆柱后得一个组合体.
如图所示,直三棱柱ABC-A1B1C1的侧棱AA1=6,底面三角形的边AB=3,BC=4,AC=5.以上、下底的内切圆为底面,挖去一个圆柱后得一个组合体. (2012•杨浦区二模)如图所示,直四棱柱ABCD-A1B1C1D1,的棱AA1长为a,底面ABCD是边长AB=2a,BC=a的矩形,E为C1D1的中点.
(2012•杨浦区二模)如图所示,直四棱柱ABCD-A1B1C1D1,的棱AA1长为a,底面ABCD是边长AB=2a,BC=a的矩形,E为C1D1的中点.