题目内容
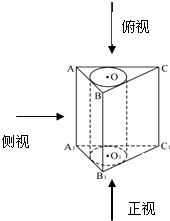 如图所示,直三棱柱ABC-A1B1C1的侧棱AA1=6,底面三角形的边AB=3,BC=4,AC=5.以上、下底的内切圆为底面,挖去一个圆柱后得一个组合体.
如图所示,直三棱柱ABC-A1B1C1的侧棱AA1=6,底面三角形的边AB=3,BC=4,AC=5.以上、下底的内切圆为底面,挖去一个圆柱后得一个组合体.(1)画出按图示方向组合体的三视图(要求标出尺寸);
(2)求组合体的体积和表面积.
分析:(1)按图示方向能作出组合体的三视图.
(2)由AC2=AB2+BC2,知△ABC为直角三角形,设△ABC内切圆半径为R,则
(3+4+5)=
×3×4,解得R=1,由此能求出组合体的体积和表面积.
(2)由AC2=AB2+BC2,知△ABC为直角三角形,设△ABC内切圆半径为R,则
| R |
| 2 |
| 1 |
| 2 |
解答:解:(1)按图示方向作出组合体的三视图为:
(2)由已知AC2=AB2+BC2,
∴△ABC为直角三角形,…(2分)
设△ABC内切圆半径为R,
则有
(3+4+5)=
×3×4,
∴R=1…(4分)
∵直三棱柱ABC-A1B1C1的体积V棱柱=S△ABC•AA1=
×3×4×6=36,…(6分)
内切圆为底面的圆柱体积V圆柱=πR2•AA1=6π,…(8分)
∴剩余部分形成的几何体的体积V=V棱柱-V圆柱=36-6π,…(10分)S直三棱柱表面=18+30+24+2×
×3×4=84;
S圆柱侧=2π×1×6=12π;
S组合体表=84+12π-2π=84+10π…(12分)

(2)由已知AC2=AB2+BC2,
∴△ABC为直角三角形,…(2分)
设△ABC内切圆半径为R,
则有
| R |
| 2 |
| 1 |
| 2 |
∴R=1…(4分)
∵直三棱柱ABC-A1B1C1的体积V棱柱=S△ABC•AA1=
| 1 |
| 2 |
内切圆为底面的圆柱体积V圆柱=πR2•AA1=6π,…(8分)
∴剩余部分形成的几何体的体积V=V棱柱-V圆柱=36-6π,…(10分)S直三棱柱表面=18+30+24+2×
| 1 |
| 2 |
S圆柱侧=2π×1×6=12π;
S组合体表=84+12π-2π=84+10π…(12分)
点评:本题考查组合体的三视图的画法,考查组合体的体积的求法,解题时要认真审题,仔细解答.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案
相关题目
 如图所示,直三棱柱ABC-A1B1C1的各条棱长均为a,D是侧棱CC1的中点.
如图所示,直三棱柱ABC-A1B1C1的各条棱长均为a,D是侧棱CC1的中点. 如图所示,直三棱柱ABC-A1B1C1中,AB⊥AC,D,E分别为AA1,B1C的中点,若记
如图所示,直三棱柱ABC-A1B1C1中,AB⊥AC,D,E分别为AA1,B1C的中点,若记 如图所示,直三棱柱ABC-A'B'C'中,∠BCA=90°,CA=CB=1,AA'=2,M,N分别是A'B'、A'A的中点.
如图所示,直三棱柱ABC-A'B'C'中,∠BCA=90°,CA=CB=1,AA'=2,M,N分别是A'B'、A'A的中点.
