题目内容
下列命题:
①函数y=sin(2x+ )的单调减区间为[kπ+
)的单调减区间为[kπ+ ,kπ+
,kπ+ ],k∈Z;
],k∈Z;
②函数y= cos2x-sin2x图象的一个对称中心为(
cos2x-sin2x图象的一个对称中心为( ,0);
,0);
③函数y=sin( x-
x- )在区间[-
)在区间[- ,
, ]上的值域为[-
]上的值域为[- ,
, ];
];
④函数y=cosx的图象可由函数y=sin(x+ )的图象向右平移
)的图象向右平移 个单位得到;
个单位得到;
⑤若方程sin(2x+ )-a=0在区间[0,
)-a=0在区间[0, ]上有两个不同的实数解x1,x2,则x1+x2=
]上有两个不同的实数解x1,x2,则x1+x2= .
.
其中正确命题的序号为 ________.
①②⑤
分析:①令 +2kπ可求
+2kπ可求
②利用两角和的余弦公式化简可得y= ,令2x+
,令2x+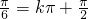 ,求出函数的对称中心
,求出函数的对称中心
③由 可得
可得 ,结合正弦函数的图象可求函数的值域
,结合正弦函数的图象可求函数的值域
④根据函数的图象平移法则:左加右减的平移法则可得
⑤根据正弦函数的图象结合函数的对称性可得.
解答:①令 +2kπ,解得
+2kπ,解得 +kπ,k∈Z,,故①正确
+kπ,k∈Z,,故①正确
②y= ,令2x+
,令2x+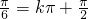 ,解得x=
,解得x= +kπ,
+kπ,
k=0时函数的一个对称中心( ,0)②正确
,0)②正确
③y= ,当-
,当-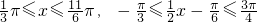 ,结合正弦函数的图象可得-
,结合正弦函数的图象可得- ≤y≤1,③错误
≤y≤1,③错误
④由函数y=sin(x+ )的图象向右平移
)的图象向右平移 个单位得到y=sinx的图象,故④错误
个单位得到y=sinx的图象,故④错误
⑤令y=sin(2x+ ),当x
),当x 时,2x+
时,2x+ ,若使方程有两解,则两解关于x=
,若使方程有两解,则两解关于x= 对称,
对称,
则x1+x2= ,故⑤正确
,故⑤正确
故答案为:①②⑤
点评:本题综合考查了三角函数y=Asin(ωx+∅)(A>0,ω>0)的性质:函数的单调区间的求解,函数的对称中心的求解,函数在闭区间上的最值的求解及函数图象的平移,还用到了两角和的余弦公式,而解决本题的关键是要熟练掌握并能灵活运用三角函数的图象.
分析:①令
 +2kπ可求
+2kπ可求②利用两角和的余弦公式化简可得y=
 ,令2x+
,令2x+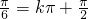 ,求出函数的对称中心
,求出函数的对称中心③由
 可得
可得 ,结合正弦函数的图象可求函数的值域
,结合正弦函数的图象可求函数的值域④根据函数的图象平移法则:左加右减的平移法则可得
⑤根据正弦函数的图象结合函数的对称性可得.
解答:①令
 +2kπ,解得
+2kπ,解得 +kπ,k∈Z,,故①正确
+kπ,k∈Z,,故①正确②y=
 ,令2x+
,令2x+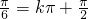 ,解得x=
,解得x= +kπ,
+kπ,k=0时函数的一个对称中心(
 ,0)②正确
,0)②正确③y=
 ,当-
,当-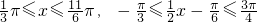 ,结合正弦函数的图象可得-
,结合正弦函数的图象可得- ≤y≤1,③错误
≤y≤1,③错误④由函数y=sin(x+
 )的图象向右平移
)的图象向右平移 个单位得到y=sinx的图象,故④错误
个单位得到y=sinx的图象,故④错误⑤令y=sin(2x+
 ),当x
),当x 时,2x+
时,2x+ ,若使方程有两解,则两解关于x=
,若使方程有两解,则两解关于x= 对称,
对称,则x1+x2=
 ,故⑤正确
,故⑤正确故答案为:①②⑤
点评:本题综合考查了三角函数y=Asin(ωx+∅)(A>0,ω>0)的性质:函数的单调区间的求解,函数的对称中心的求解,函数在闭区间上的最值的求解及函数图象的平移,还用到了两角和的余弦公式,而解决本题的关键是要熟练掌握并能灵活运用三角函数的图象.

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案
相关题目