题目内容
16．已知圆M1：（x+4）2+y2=25，圆M2：x2+（y-3）2=1，一动圆P与这两个圆都外切，试求动圆圆心P的轨迹．分析 设动圆P的半径为r，然后根据动圆与圆M1：（x+4）2+y2=25，圆M2：x2+（y-3）2=1都外切，得|PM1|=5+r，|PM2|=1+r，再两式相减消去参数r，则满足双曲线的定义，问题解决．
解答 解：设动圆的圆心为P，半径为r，
而圆M1：（x+4）2+y2=25的圆心为O（-4，0），半径为5；
圆M2：x2+（y-3）2=1的圆心为F（0，3），半径为1．
依题意得|PM1|=5+r，|PM2|=1+r，
则|PM1|-|PM2|=（5+r）-（1+r）=4＜|M1M2|，
所以点P的轨迹是双曲线的右支．
点评 本题主要考查双曲线的定义．解题的关键是根据已知条件中未知圆与已知圆的位置关系，结合“圆的位置关系与半径及圆心距的关系”，探究出动圆圆心P的轨迹．
练习册系列答案
相关题目
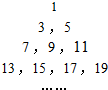将正奇数排成如图所示的三角形数表：
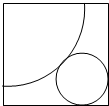如图，在边长为5+$\sqrt{2}$的正方形纸片中剪下如图所示的扇形和圆，使它恰好成同一圆锥的侧面和底面，求此圆锥的体积．