题目内容
4.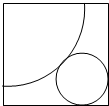 如图,在边长为5+$\sqrt{2}$的正方形纸片中剪下如图所示的扇形和圆,使它恰好成同一圆锥的侧面和底面,求此圆锥的体积.
如图,在边长为5+$\sqrt{2}$的正方形纸片中剪下如图所示的扇形和圆,使它恰好成同一圆锥的侧面和底面,求此圆锥的体积.
分析 设小圆半径为r,可求得小圆的周长,利用扇形的弧长公式可得大扇形的半径,根据大扇形的半径+小扇形的半径+小扇形半径的$\sqrt{2}$倍=正方形对角线长,能求出小扇形的半径,从而能求出圆锥的底面半径,由此能求出此圆锥的体积.
解答  解:如图,在边长为5+$\sqrt{2}$的正方形纸片中,
解:如图,在边长为5+$\sqrt{2}$的正方形纸片中,
AC=$\sqrt{(5+\sqrt{2})^{2}+(5+\sqrt{2})^{2}}$=2+5$\sqrt{2}$,
设小圆半径为r,则小圆周长为2πr,
∵在边长为5+$\sqrt{2}$的正方形纸片中剪下扇形和圆,
∴△OCD是等腰直角三角形,则OC=$\sqrt{2}r$,
设大圆半径为x,则$\frac{90π×x}{180}$=2πr,解得x=4r,
∴4r+r+$\sqrt{2}r$=$\sqrt{(5+\sqrt{2})^{2}+(5+\sqrt{2})^{2}}$,
解得r=$\sqrt{2}$,x=4$\sqrt{2}$,
∴圆锥的高h=$\sqrt{30}$,
∴圆锥体积V=$\frac{1}{3}π{r}^{2}h$=$\frac{2π\sqrt{30}}{3}$.
点评 本题考查圆锥体积的求法,是中档题,解题时要认真审题,根据正方形对角线长得到关系式:大扇形的半径+小扇形的半径+小扇形半径的$\sqrt{2}$倍=正方形对角线长是解决本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
19.设a>b>0,当a2+$\frac{4}{b(a-b)}$取得最小值时,函数f(x)=$\frac{a}{si{n}^{2}x}$+bsin2x的最小值为( )
| A. | 3 | B. | 2$\sqrt{2}$ | C. | 5 | D. | 4$\sqrt{2}$ |
13.下列结论中正确的是( )
| A. | 如果直线l垂直于平面α内的无数条直线,那么l⊥α | |
| B. | 如果直线1平行于平面α内的无数条直线,那么l∥α | |
| C. | 过空间一点有且只有一条直线平行于已知平面 | |
| D. | 过空间一点有且只有一条直线垂直于已知平面 |
 长方体ABCD-A1B1C1D1中,AB=BC=1,AA1=2,E、F分别为侧棱BB1、CC1的中点,求四棱锥B-A1EFD1的体积.
长方体ABCD-A1B1C1D1中,AB=BC=1,AA1=2,E、F分别为侧棱BB1、CC1的中点,求四棱锥B-A1EFD1的体积.