题目内容
如图示,AB是圆柱的母线,BD是圆柱底面圆的直径,C是底面圆周上一点,E是AC中点,且AB=BC=2,∠CBD=45°.
(1)求证:CD⊥面ABC;
(2)求直线BD与面ACD所成角的大小.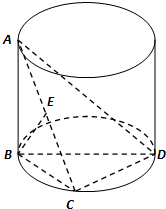
(1)求证:CD⊥面ABC;
(2)求直线BD与面ACD所成角的大小.

(1)证明:∵BD是底面圆的直径,∴∠BCD=90°,∴CD⊥BC;
由圆柱可得:母线AB⊥底面BCD,∴AB⊥CD;
又AB∩BC=B,∴CD⊥平面ABC.
(2)连接DE,由(1)可知:CD⊥BE.
∵E是AC的中点,AB=BC,∠ABC=90°.
∴BE⊥AC,
又AC∩CD=C,∴BE⊥平面ACD.
∴∠BDE是直线BD与面ACD所成的角.
在Rt△ABC中,AB=BC=2,AE=EC,∴BE=
AC=
×
=
,
在Rt△BCD中,BC=2,∠CBD=45°,∴BD=2
.
由BE⊥平面ACD,∴BE⊥ED,即∠BED=90°.
∴sin∠BDE=
=
=
,
又∠BDE是锐角,∴∠BDE=30°.
由圆柱可得:母线AB⊥底面BCD,∴AB⊥CD;
又AB∩BC=B,∴CD⊥平面ABC.
(2)连接DE,由(1)可知:CD⊥BE.
∵E是AC的中点,AB=BC,∠ABC=90°.
∴BE⊥AC,
又AC∩CD=C,∴BE⊥平面ACD.
∴∠BDE是直线BD与面ACD所成的角.
在Rt△ABC中,AB=BC=2,AE=EC,∴BE=
| 1 |
| 2 |
| 1 |
| 2 |
| 22×2 |
| 2 |
在Rt△BCD中,BC=2,∠CBD=45°,∴BD=2
| 2 |
由BE⊥平面ACD,∴BE⊥ED,即∠BED=90°.
∴sin∠BDE=
| BE |
| BD |
| ||
2
|
| 1 |
| 2 |
又∠BDE是锐角,∴∠BDE=30°.

练习册系列答案
相关题目
 如图示,AB是圆柱的母线,BD是圆柱底面圆的直径,C是底面圆周上一点,E是AC中点,且AB=BC=2,∠CBD=45°.
如图示,AB是圆柱的母线,BD是圆柱底面圆的直径,C是底面圆周上一点,E是AC中点,且AB=BC=2,∠CBD=45°.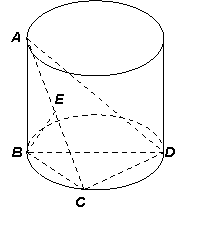
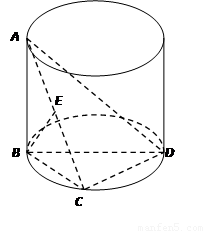
 .
.
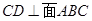 ;
;