题目内容
幂函数y=f(x)的图象经过点(2, ),则满足f(x)=-27的x的值是 .
),则满足f(x)=-27的x的值是 .
【答案】分析:设幂函数f(x)=xa,由幂函数y=f(x)的图象经过点(2, ),解得a=-3,由此能求出满足f(x)=-27的x的值.
),解得a=-3,由此能求出满足f(x)=-27的x的值.
解答:解:设幂函数f(x)=xa,
∵幂函数y=f(x)的图象经过点(2, ),
),
∴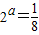 ,解得a=-3,
,解得a=-3,
∴f(x)=x-3,
∵f(x)=x-3=-27,
∴x=- .
.
故答案为:- .
.
点评:本题考查幂函数的性质的应用,是基础题.解题时要认真审题,仔细解答.
 ),解得a=-3,由此能求出满足f(x)=-27的x的值.
),解得a=-3,由此能求出满足f(x)=-27的x的值.解答:解:设幂函数f(x)=xa,
∵幂函数y=f(x)的图象经过点(2,
 ),
),∴
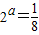 ,解得a=-3,
,解得a=-3,∴f(x)=x-3,
∵f(x)=x-3=-27,
∴x=-
 .
.故答案为:-
 .
.点评:本题考查幂函数的性质的应用,是基础题.解题时要认真审题,仔细解答.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目