题目内容
已知向量a=(sinx,2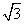 sinx),b=(2cosx,sinx),定义f(x)=a·b-
sinx),b=(2cosx,sinx),定义f(x)=a·b-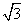 。
。
(1)求函数y=f(x),x∈R的单调递减区间;
(2)若函数y=f(x+θ)(0<θ<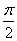 )为偶函数,求θ的值。
)为偶函数,求θ的值。
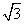 sinx),b=(2cosx,sinx),定义f(x)=a·b-
sinx),b=(2cosx,sinx),定义f(x)=a·b-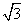 。
。(1)求函数y=f(x),x∈R的单调递减区间;
(2)若函数y=f(x+θ)(0<θ<
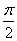 )为偶函数,求θ的值。
)为偶函数,求θ的值。解:f(x)=2sinxcosx+2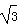 sin2x-
sin2x-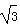
=sin2x+2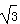 ·
·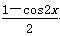 -
-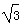 =sin2x-
=sin2x-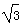 cos2x
cos2x
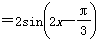 。
。
(1)令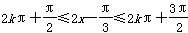
解得f(x)的单调递减区间是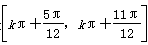 ,k∈Z。
,k∈Z。
(2)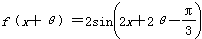
根据三角函数图象性质可知
y=f(x+θ)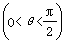 在x=0处取最值
在x=0处取最值
即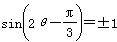
∴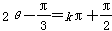 ,
,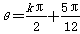 ,k∈Z
,k∈Z
又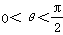
∴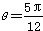 。
。
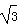 sin2x-
sin2x-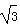
=sin2x+2
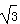 ·
·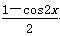 -
-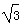 =sin2x-
=sin2x-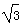 cos2x
cos2x 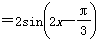 。
。(1)令
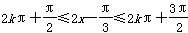
解得f(x)的单调递减区间是
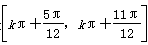 ,k∈Z。
,k∈Z。(2)
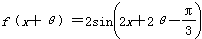
根据三角函数图象性质可知
y=f(x+θ)
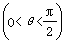 在x=0处取最值
在x=0处取最值即
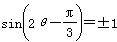
∴
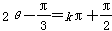 ,
,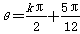 ,k∈Z
,k∈Z又
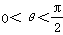
∴
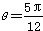 。
。
练习册系列答案
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案 品学双优卷系列答案
品学双优卷系列答案
相关题目