题目内容
直线l：y=k(x+2)被圆O：x2+y2=4截得弦长为2，则A值是( )A．±
B．±
C．±
D．±
答案：C 【解析】本题考查直线与圆的位置关系，考查学生数形结合思想、方程思想．有两种解法，方法一：图像法．如图，
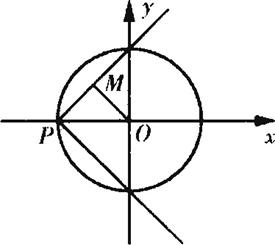
直线过定点P(-2，0)，定圆的圆心在原点，半径为2，设相交弦的中点为M，则OM⊥PM 且PM=1，OP=2，在直角三角形POM中，可解得∠MPO=60°，故k=±．
方法二：代数法．在直角三角形POM中，因为可以求得OM=，即点O到直线y=k(x+2)的距离为，利用点到直线的距离公式可得．
练习册系列答案
一线名师提优试卷系列答案
相关题目
已知直线l：y=k(x-1)-
与圆x2+y2=1相切，则直线l的倾斜角为（ ）
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
与圆O：x2+y2=4相交于A,B两点，O为坐标原点，△AOB的面积为S。(1)试将S表示为k的函数S(k)，并求出它的义域；求S的最大值，并求出此时的k值。