题目内容
已知椭圆的中心在原点,焦点在y轴上,焦距为4,离心率为 .
.(Ⅰ)求椭圆的方程;
(Ⅱ)设椭圆在y轴的正半轴上的焦点为M,又点A和B在椭圆上,且M分有向线段
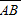 所成的比为2,求线段AB所在直线的方程.
所成的比为2,求线段AB所在直线的方程.
【答案】分析:(Ⅰ)设椭圆方程,由焦距为4,离心率为 ,结合b2=a2-c2,即可求得椭圆方程;
,结合b2=a2-c2,即可求得椭圆方程;
(Ⅱ)先考虑A点在B点的左方,利用M分有向线段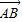 所成的比为2,结合椭圆的定义,即可求得A,B的坐标,从而可得直线AB的斜率,进而可得AB的方程;点在B的右方时根据对称性,可得所求直线AB的方程.
所成的比为2,结合椭圆的定义,即可求得A,B的坐标,从而可得直线AB的斜率,进而可得AB的方程;点在B的右方时根据对称性,可得所求直线AB的方程.
解答:解:(Ⅰ)设椭圆方程为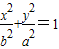 (b>a>0)(1分)
(b>a>0)(1分)
由焦距为4,可得2c=4,∴c=2,
又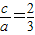 ,故a=3(2分)
,故a=3(2分)
∴b2=a2-c2=5,
∴所求椭圆方程为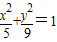 (3分)
(3分)
(Ⅱ)M坐标为(0,2),设A点在B点的左方,且A(x1,y1),B(x2,y2),
由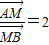 ,故有
,故有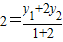 (5分)即y1+2y2=6,
(5分)即y1+2y2=6,
又M相应的准线方程是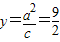 ,A到准线距离
,A到准线距离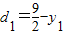 ,B到准线距离
,B到准线距离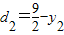 (6分),
(6分),
∵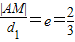 ,
,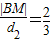 (7分)
(7分)
∴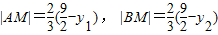 ,
,
∴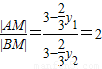 得4y2-2y1=9②
得4y2-2y1=9②
②与①联立解得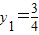 ,代入椭圆方程得
,代入椭圆方程得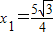 ,
,
∴直线AB的斜率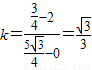 (9分),
(9分),
∴AB的方程为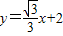 (10分),
(10分),
如果点在B的右方时根据对称性,则所求直线AB的方程为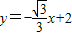 .(12分)
.(12分)
点评:本题考查椭圆的标准方程,考查椭圆的定义,考查向量知识的运用,考查学生的计算能力,确定A,B的坐标是关键.
 ,结合b2=a2-c2,即可求得椭圆方程;
,结合b2=a2-c2,即可求得椭圆方程;(Ⅱ)先考虑A点在B点的左方,利用M分有向线段
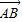 所成的比为2,结合椭圆的定义,即可求得A,B的坐标,从而可得直线AB的斜率,进而可得AB的方程;点在B的右方时根据对称性,可得所求直线AB的方程.
所成的比为2,结合椭圆的定义,即可求得A,B的坐标,从而可得直线AB的斜率,进而可得AB的方程;点在B的右方时根据对称性,可得所求直线AB的方程.解答:解:(Ⅰ)设椭圆方程为
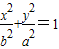 (b>a>0)(1分)
(b>a>0)(1分) 由焦距为4,可得2c=4,∴c=2,
又
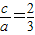 ,故a=3(2分)
,故a=3(2分)∴b2=a2-c2=5,
∴所求椭圆方程为
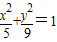 (3分)
(3分)(Ⅱ)M坐标为(0,2),设A点在B点的左方,且A(x1,y1),B(x2,y2),
由
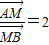 ,故有
,故有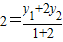 (5分)即y1+2y2=6,
(5分)即y1+2y2=6,又M相应的准线方程是
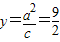 ,A到准线距离
,A到准线距离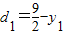 ,B到准线距离
,B到准线距离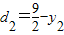 (6分),
(6分),∵
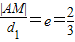 ,
,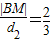 (7分)
(7分)∴
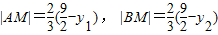 ,
,∴
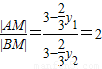 得4y2-2y1=9②
得4y2-2y1=9②②与①联立解得
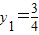 ,代入椭圆方程得
,代入椭圆方程得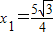 ,
,∴直线AB的斜率
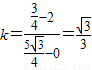 (9分),
(9分),∴AB的方程为
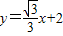 (10分),
(10分),如果点在B的右方时根据对称性,则所求直线AB的方程为
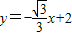 .(12分)
.(12分)点评:本题考查椭圆的标准方程,考查椭圆的定义,考查向量知识的运用,考查学生的计算能力,确定A,B的坐标是关键.

练习册系列答案
相关题目