题目内容
如图,已知长方形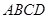 的两条对角线的交点为
的两条对角线的交点为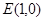 ,且
,且 与
与 所在的直线方程分别为
所在的直线方程分别为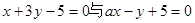 .
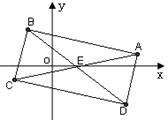
.
(1)求 所在的直线方程;
所在的直线方程;
(2)求出长方形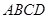 的外接圆的方程.
的外接圆的方程.
(1) ;(2)
;(2) .
.
解析试题分析:(1)由已知条件推导出 ,设
,设 所在的直线
所在的直线
方程为 ,由
,由 到
到 的距离和
的距离和 到
到 的距离相等,能求出
的距离相等,能求出 所在的直线方程.
所在的直线方程.
(2)由 ,得
,得 ,从而得到
,从而得到 ,由此能求出长方形
,由此能求出长方形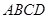 的外接圆的方程.
的外接圆的方程.
试题解析:(1)由于 ,则
,则
由于 ,则可设直线
,则可设直线 的方程为:
的方程为: ,
,
又点 到
到 与
与 的距离相等,则
的距离相等,则 ,
,
因此, ,或
,或 (舍去),
(舍去),
则直线 所在的方程为
所在的方程为 .
.
(2)由直线 的方程解出点
的方程解出点 的坐标为
的坐标为 ,则
,则 即为长方形
即为长方形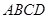 的外接圆半径.故长方形
的外接圆半径.故长方形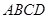 的外接圆的方程为
的外接圆的方程为 .
.
考点:圆的标准方程;直线的一般式方程.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
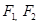 为椭圆
为椭圆 :
: 的左、右焦点,过椭圆右焦点F2斜率为
的左、右焦点,过椭圆右焦点F2斜率为 (
(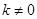 )的直线
)的直线 与椭圆
与椭圆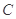 相交于
相交于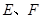 两点,
两点,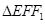 的周长为8,且椭圆C与圆
的周长为8,且椭圆C与圆 相切。
相切。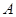 为椭圆的右顶点,直线
为椭圆的右顶点,直线 分别交直线
分别交直线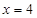 于点
于点 ,线段
,线段 的中点为
的中点为 ,记直线
,记直线 的斜率为
的斜率为 ,求证
,求证 为定值.
为定值.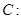
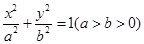 上的点到椭圆右焦点
上的点到椭圆右焦点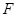 的最大距离为
的最大距离为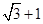 ,离心率
,离心率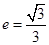 ,直线
,直线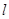 过点
过点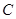 交于
交于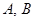 两点.
两点.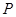 ,使得当
,使得当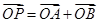 成立?若存在,求出所有点
成立?若存在,求出所有点 与
与 平行,则
平行,则 ___________.
___________.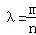 ,△BDM和△ABN的面积分别为S1和S2.
,△BDM和△ABN的面积分别为S1和S2.