题目内容
已知（1-2x）7=a0+a1x+a2x2+a3x3+…+a7x7．
（1）求a1+a2+a3+…+a7的值．
（2）求a1+a3+a5+a7的值．
（1）求a1+a2+a3+…+a7的值．
（2）求a1+a3+a5+a7的值．
考点：二项式系数的性质
专题：二项式定理
分析：（Ⅰ）在所给的等式中，令x=1得：a0+a1+…+a7=-1，再令x=0得：a0=1，从而求得a1+a2+…+a7 的值．
（Ⅱ）在所给的等式中，令x=-1得：a0-a1+a2-a3+…-a7=37，再利用a0+a1+…+a7=-1，可得 a1+a3+a5+a7的值．
（Ⅱ）在所给的等式中，令x=-1得：a0-a1+a2-a3+…-a7=37，再利用a0+a1+…+a7=-1，可得 a1+a3+a5+a7的值．
解答：
解：（Ⅰ）在（1-2x）7=a0+a1x+a2x2+a3x3+…+a7x7中，令x=1得：a0+a1+…+a7=-1，
再令x=0得：a0=1，所以a1+a2+…+a7=-2．
（Ⅱ）令x=-1得：a0-a1+a2-a3+…-a7=37，再利用a0+a1+…+a7=-1，可得：2（a1+a3+a5+a7）=-1-37 ，
所以a1+a3+a5+a7=
．
再令x=0得：a0=1，所以a1+a2+…+a7=-2．
（Ⅱ）令x=-1得：a0-a1+a2-a3+…-a7=37，再利用a0+a1+…+a7=-1，可得：2（a1+a3+a5+a7）=-1-37 ，
所以a1+a3+a5+a7=
| -1-37 |
| 2 |
点评：本题主要考查二项式定理的应用，是给变量赋值的问题，关键是根据要求的结果，选择合适的数值代入，属于基题．
练习册系列答案
相关题目
如图是函数y=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜| π |
| 2 |
| OM |
| ON |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
△ABC的内角A，B，C的对边分别为a，b，c．若c=
，b=
，B=120°，则sinC等于（ ）
| 2 |
| 6 |
A、
| ||||
| B、2 | ||||
C、
| ||||
D、
|
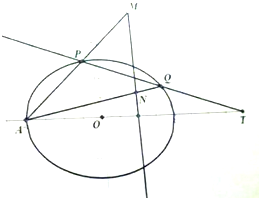已知椭圆
高尔顿板是英国生物统计学家高尔顿设计用来研究随机现象的模型，在一块木板上钉着若干排相互平行但相互错开的圆柱形小木块，小木块之间留有适当的空隙作为通道，前面挡有一块玻璃．让一个小球从高尔顿板上方的通道口落下，小球在下落的过程中与层层小木块碰撞，且等可能向左或向右滚下，最后掉入高尔顿板下方的某一球槽内．如图所示的高尔顿板有7层小木块，小球从通道口落下，第一次与第2层中间的小木块碰撞，以