题目内容
18.某三棱锥的三视图如图所示,其侧(左)视图为直角三角形,则该三棱锥最长的棱长等于( )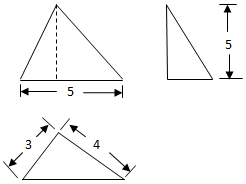
| A. | $4\sqrt{2}$ | B. | $\sqrt{34}$ | C. | $\sqrt{41}$ | D. | $5\sqrt{2}$ |
分析 根据几何体的三视图,得:该几何体是底面为直角三角形,侧面垂直于底面,高为5的三棱锥,即可求得.
解答 解:根据几何体的三视图,得:该几何体是底面为直角三角形,侧面垂直于底面,高为5的三棱锥,
棱锥最长的棱长等于$\sqrt{25+16}$=$\sqrt{41}$,
故选C.
点评 本题考查了空间几何体的三视图的应用问题,比较基础

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目
8.设变量x,y满足约束条件$\left\{\begin{array}{l}x+2y-4≤0\\ 3x+y-3≥0\\ x-y-1≤0\end{array}\right.$,则$z=\frac{y}{x+1}$的最大值为( )
| A. | $\frac{9}{7}$ | B. | $\frac{1}{3}$ | C. | 0 | D. | 2 |
9.若a<b<0,那么下列不等式成立的是( )
| A. | ab<b2 | B. | a2<b2 | C. | lg(-ab)<lg(-a2) | D. | 2${\;}^{\frac{1}{b}}$<2${\;}^{\frac{1}{a}}$ |
6.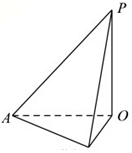 如图,有一建筑物OP,为了测量它的高度,在地面上选一长度为40m的基线AB,若在点A处测得P点的仰角为30°,在B点处的仰角为45°,且∠AOB=30°,则建筑物的高度为( )
如图,有一建筑物OP,为了测量它的高度,在地面上选一长度为40m的基线AB,若在点A处测得P点的仰角为30°,在B点处的仰角为45°,且∠AOB=30°,则建筑物的高度为( )
 如图,有一建筑物OP,为了测量它的高度,在地面上选一长度为40m的基线AB,若在点A处测得P点的仰角为30°,在B点处的仰角为45°,且∠AOB=30°,则建筑物的高度为( )
如图,有一建筑物OP,为了测量它的高度,在地面上选一长度为40m的基线AB,若在点A处测得P点的仰角为30°,在B点处的仰角为45°,且∠AOB=30°,则建筑物的高度为( )| A. | 20m | B. | 20$\sqrt{2}$m | C. | 20$\sqrt{3}$m | D. | 40m |
7.某校随机调查了110名不同性别的学生每天在校的消费情况,规定:50元以下为正常消费,大于或等于50元为非正常消费.统计后,得到如下的2×2列联表,已知在调查对象中随机抽取1人,为非正常消费的概率为$\frac{3}{11}$.
(Ⅰ)请完成上面的列联表;
(Ⅱ)根据列联表的数据,能否有99%的把握认为消费情况与性别有关系?
附临界值表参考公式:
${K^2}=\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$,其中n=a+b+c+d.
| 正常 | 非正常 | 合计 | |
| 男 | 30 | 20 | 50 |
| 女 | 50 | 10 | 60 |
| 合计 | 80 | 30 | 110 |
(Ⅱ)根据列联表的数据,能否有99%的把握认为消费情况与性别有关系?
附临界值表参考公式:
| P(K2≥k0) | 0.100 | 0.05 | 0.025 | 0.010 | 0.001 |
| k0 | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
8.口袋中装有一些大小相同的红球、白球和黑球,从中摸出一个球,摸出红球的概率是0.43,摸出白球的概率是0.27,那么摸出黑球的概率是( )
| A. | 0.43 | B. | 0.27 | C. | 0.3 | D. | 0.7 |
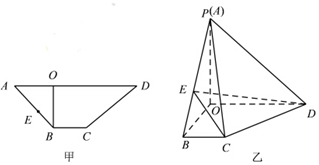
 如图,在圆内接四边形ABCD中,AB=2,AD=1,$\sqrt{3}$BC=$\sqrt{3}$BDcosα+CDsinβ,则四边形ABCD周长的取值范围为(3+$\sqrt{7}$,3+2$\sqrt{7}$).
如图,在圆内接四边形ABCD中,AB=2,AD=1,$\sqrt{3}$BC=$\sqrt{3}$BDcosα+CDsinβ,则四边形ABCD周长的取值范围为(3+$\sqrt{7}$,3+2$\sqrt{7}$).