题目内容
(本小题满分12分)
已知数列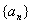 满足
满足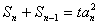 (t>0,n≥2),且
(t>0,n≥2),且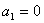 ,n≥2时,
,n≥2时,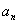 >0.其中
>0.其中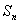 是数列
是数列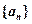 的前n项和.
的前n项和.
(Ⅰ)求数列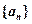 的通项公式;
的通项公式;
(Ⅱ)若对于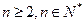 ,不等式
,不等式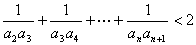 恒成立,求t 的取值范围.
恒成立,求t 的取值范围.
已知数列
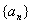 满足
满足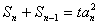 (t>0,n≥2),且
(t>0,n≥2),且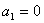 ,n≥2时,
,n≥2时,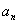 >0.其中
>0.其中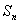 是数列
是数列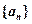 的前n项和.
的前n项和.(Ⅰ)求数列
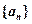 的通项公式;
的通项公式; (Ⅱ)若对于
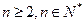 ,不等式
,不等式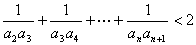 恒成立,求t 的取值范围.
恒成立,求t 的取值范围.解:(Ⅰ)依 题意,
题意,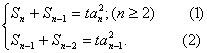 , (1)-(2)
, (1)-(2)
得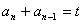 (
(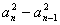 )(n≥3),由已知
)(n≥3),由已知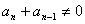 ,故
,故 =(n≥3),
=(n≥3),
由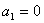 ,
, 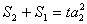 ,得
,得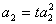 ,
,  ,
,
即数列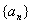 从第二项开始是首项为
从第二项开始是首项为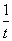 ,公差为的等差数列.
,公差为的等差数列.
所以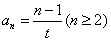 ,又当
,又当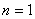 时,
时, ,
,
所以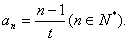 。
。
(Ⅱ)设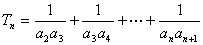
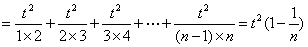
要使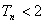 ,对于
,对于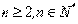 恒成立, 只要
恒成立, 只要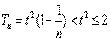 成立, 所以
成立, 所以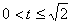
 题意,
题意,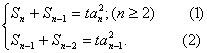 , (1)-(2)
, (1)-(2)得
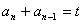 (
(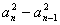 )(n≥3),由已知
)(n≥3),由已知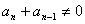 ,故
,故 =(n≥3),
=(n≥3), 由
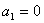 ,
, 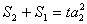 ,得
,得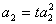 ,
,  ,
, 即数列
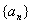 从第二项开始是首项为
从第二项开始是首项为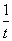 ,公差为的等差数列.
,公差为的等差数列.所以
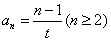 ,又当
,又当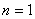 时,
时, ,
,所以
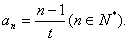 。
。(Ⅱ)设
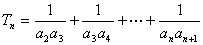
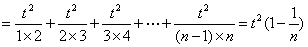
要使
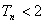 ,对于
,对于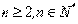 恒成立, 只要
恒成立, 只要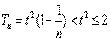 成立, 所以
成立, 所以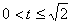
略

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
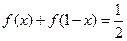 .
.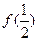 的值.
的值.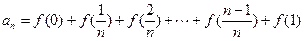 ,数列
,数列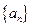 是等差数列吗?如果是请给予证明,不是请说明理由。
是等差数列吗?如果是请给予证明,不是请说明理由。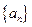 的前
的前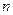 项和为
项和为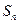 ,
,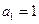 ,
,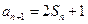 ,等差数列
,等差数列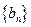 满足
满足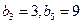 ,(1)分别求数列
,(1)分别求数列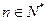 ,
,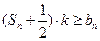 恒成立,求实数
恒成立,求实数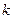 的取值范围.
的取值范围.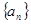 的通项公式为
的通项公式为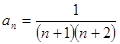 ,其前
,其前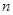 项和为
项和为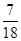 ,则
,则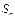 是数列{an}的前n项和
是数列{an}的前n项和 ,则
,则 ,则该数列的前2011项的乘积
,则该数列的前2011项的乘积 ( )
( )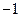 .
. .
.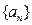 的通项公式是
的通项公式是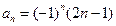 ,则它的前51项和是 ( )
,则它的前51项和是 ( )
 的通项公式
的通项公式 ,设
,设 项的和为
项的和为 ,则使
,则使 成立的自然数
成立的自然数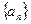 中,
中,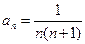 ,前n项和为Sn,则S2009=______________。
,前n项和为Sn,则S2009=______________。