题目内容
已知直角坐标平面内两点A(x,
-x),B(
,0),那么这两点之间距离的最小值等于
.
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
分析:先根据两点间的距离公式d=
,计算点A与点B间的距离,再利用二次函数的性质求出其最小值即可.
| (x2-x1)2+(y2-y1)2 |
解答:解:∵在平面直角坐标系内,两点A(x,
-x),B(
,0),
∴|AB|=
=
≥
,
当x=
时,取等号.
故答案是:
.
| 2 |
| ||
| 2 |
∴|AB|=
(x-
|
2(x-
|
| 1 |
| 2 |
当x=
3
| ||
| 4 |
故答案是:
| 1 |
| 2 |
点评:本题考查了两点间的距离公式.解答该题时,也可以将点A与点B在平面直角坐标系中找出来,然后根据“数形结合”的数学思想解题.

练习册系列答案
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案
相关题目
 已知直角坐标平面内的动点M满足:|MA|2-|MB|2=4(|MB|-1),其中A(0,-1),B(0,1).
已知直角坐标平面内的动点M满足:|MA|2-|MB|2=4(|MB|-1),其中A(0,-1),B(0,1). ,
, ,使得平面内任何一个向量
,使得平面内任何一个向量 都可以唯一表示成
都可以唯一表示成 ,则
,则 的取值范围是(
)
的取值范围是(
) B.
B. C.
C. D.
D. [网
[网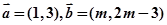 ,使得平面内的任意一个向量
,使得平面内的任意一个向量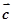 都可以唯一的表示成
都可以唯一的表示成 ,则
,则 的取值范围是 .
的取值范围是 .