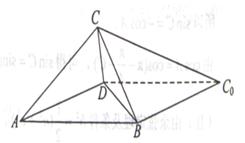
题目内容
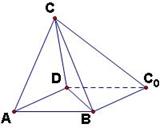
如图,一张平行四边形的硬纸片 中,
中, ,
, 。沿它的对角线
。沿它的对角线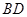 把△
把△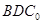 折起,使点
折起,使点 到达平面
到达平面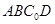 外点
外点 的位置。
的位置。
(Ⅰ)△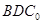 折起的过程中,判断平面
折起的过程中,判断平面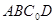 与平面
与平面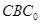 的位置关系,并给出证明;
的位置关系,并给出证明;
(Ⅱ)当△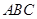 为等腰三角形,求此时二面角
为等腰三角形,求此时二面角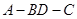 的大小。
的大小。
【答案】
(Ⅰ)平面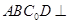 平面
平面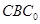 …………1分
…………1分
证明:因为
 ,
,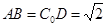 ,所以
,所以 ,
,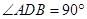 。
。
因为折叠过程中,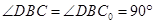 ,所以
,所以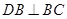 ,又
,又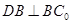 ,故
,故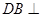 平面
平面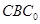 。
。
又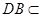 平面
平面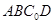 ,所以平面
,所以平面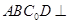 平面
平面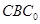 。…………5分
。…………5分
(Ⅱ)解法一:如图,延长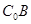 到
到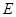 ,使
,使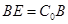 ,连结
,连结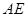 ,
, 。…………6分
。…………6分
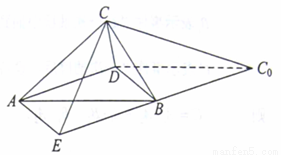
因为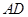

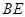 ,
,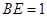 ,
,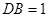 ,
,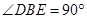 ,所以
,所以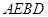 为正方形,
为正方形,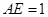 。
。
由于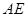 ,
,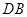 都与平面
都与平面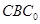 垂直,所以
垂直,所以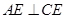 ,可知
,可知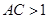 。
。
因此只有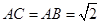 时,△
时,△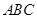 为等腰三角形。………………8分
为等腰三角形。………………8分
在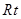 △
△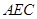 中,
中,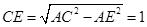 ,
,
又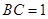 ,所以△
,所以△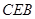 为等边三角形,
为等边三角形,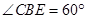 。………………10分
。………………10分
由(Ⅰ)可知,,所以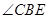 为二面角
为二面角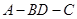 的平面角,即二面角
的平面角,即二面角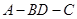 的大为
的大为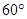 。…………12
。…………12
解法二:以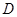 为坐标原点,射线
为坐标原点,射线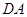 ,
,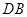 分别为
分别为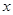 轴正半轴和
轴正半轴和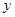 轴正半轴,建立如图的空间直角坐标系
轴正半轴,建立如图的空间直角坐标系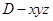 ,则
,则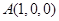 ,
,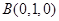 ,
,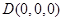 。………………6分
。………………6分
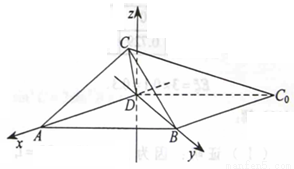
由(Ⅰ)可设点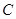 的坐标为
的坐标为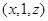 ,其中
,其中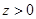 ,则有
,则有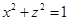 。 ①
。 ①
因为△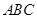 为等腰三角形,
为等腰三角形,
所以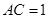 或
或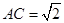 。………………8分
。………………8分
若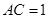 ,则有
,则有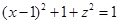 。
。
则此得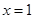 ,
,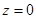 ,不合题意。
,不合题意。
若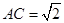 ,则有
,则有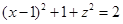 。 ②
。 ②
联立①和②得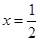 ,
,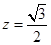 。故点
。故点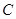 的坐标为
的坐标为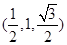 。
。
由于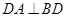 ,
,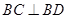 ,所以
,所以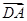 与
与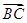 夹角的大小等于二面角
夹角的大小等于二面角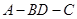 的大小。
的大小。
又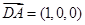 ,
,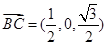 ,
,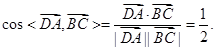
所以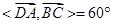 ,即二面角
,即二面角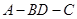 的大小为
的大小为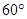 。
。
【解析】略

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
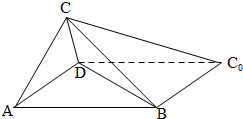 如图,一张平行四边形的硬纸片ABC0D中,AD=BD=1,
如图,一张平行四边形的硬纸片ABC0D中,AD=BD=1,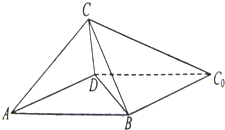 如图,一张平行四边形的硬纸片ABC0D中,AD=BD=1,
如图,一张平行四边形的硬纸片ABC0D中,AD=BD=1, 中,
中,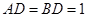 ,
,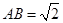 。沿它的对角线
。沿它的对角线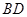 把△
把△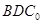 折起,使点
折起,使点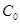 到达平面
到达平面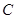 的位置。
的位置。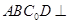 平面
平面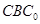 ;
;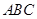 为等腰三角形,求二面角
为等腰三角形,求二面角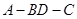 的大小。
的大小。