题目内容
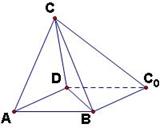
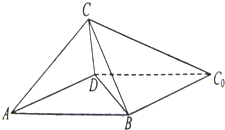 如图,一张平行四边形的硬纸片ABC0D中,AD=BD=1,AB=
如图,一张平行四边形的硬纸片ABC0D中,AD=BD=1,AB=| 2 |
(Ⅰ)△BDC0折起的过程中,判断平面ABC0D与平面CBC0的位置关系,并给出证明;
(Ⅱ)当△ABC为等腰三角形,求此时二面角A-BD-C的大小.
分析:(I)用勾股定理的逆定理,可证出AD⊥DB,C0B⊥DB.因为在折叠过程中,所以DB始终与BC垂直,根据线面垂直的判定定理可得DB⊥平面CBC0,最后用面面垂直的判定定理可得到平面ABC0D与平面CBC0互相垂直.
(II)以D为坐标原点,射线DA,DB分别为x轴正半轴和y轴正半轴,建立空间直角坐标系,从而得出A、B、D各点的坐标,再设点C(x,1,z),其中z>0,根据BC=1和△ABC为等腰三角形建立关于x、z方程组,解之可得点C的坐标为(
,1,
).最后用空间向量夹角的坐标公式,求出向量
与
夹角为60°,即为二面角A-BD-C的大小.
(II)以D为坐标原点,射线DA,DB分别为x轴正半轴和y轴正半轴,建立空间直角坐标系,从而得出A、B、D各点的坐标,再设点C(x,1,z),其中z>0,根据BC=1和△ABC为等腰三角形建立关于x、z方程组,解之可得点C的坐标为(
| 1 |
| 2 |
| ||
| 2 |
| DA |
| BC |
解答:解:(Ⅰ)结论:平面ABC0D⊥平面CBC0…(1分)
证明:∵AD=BD=1,AB=
.
∴AD2+BD2=2=AB2,可得∠ADB=90°,即AD⊥DB
∵四边形ABC0D是平行四边形,∴AD∥C0B,可得C0B⊥DB.
而在折叠过程中,∠DBC=∠DBC0=90°不变,所以DB⊥BC,
又∵DB⊥BC0,BC、BC0是平面CBC0内的相交直线,∴DB⊥平面CBC0.
∵DB?平面ABC0D,所以平面ABC0D⊥平面CBC0.…(5分)
(Ⅱ)以D为坐标原点,射线DA,DB分别为x轴正半轴和y轴正半轴,建立如图的空间直角坐标系D-xyz,
则A(1,0,0),B(0,1,0),D(0,0,0).…(6分)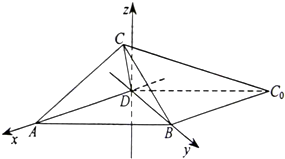
由(Ⅰ)可设点C的坐标为(x,1,z),其中z>0,
则有x2+z2=1. ①
因为△ABC为等腰三角形,
所以AC=1或AC=
.…(8分)
若AC=1,则有(x-1)2+1+z2=1.
则此得x=1,z=0,不合题意.
若AC=
,则有(x-1)2+1+z2=2. ②
联立①和②得x=
,z=
.
因此点C的坐标为(
,1,
).
由于DA⊥BD,BC⊥BD,所以
与
夹角的大小等于二面角A-BD-C的大小.
∵
=(1,0,0),
=(
,0,
),
∴cos<
,
>=
=
.
所以<
,
>=60°,即二面角A-BD-C的大小为60°.…(12分)
证明:∵AD=BD=1,AB=
| 2 |
∴AD2+BD2=2=AB2,可得∠ADB=90°,即AD⊥DB
∵四边形ABC0D是平行四边形,∴AD∥C0B,可得C0B⊥DB.
而在折叠过程中,∠DBC=∠DBC0=90°不变,所以DB⊥BC,
又∵DB⊥BC0,BC、BC0是平面CBC0内的相交直线,∴DB⊥平面CBC0.
∵DB?平面ABC0D,所以平面ABC0D⊥平面CBC0.…(5分)
(Ⅱ)以D为坐标原点,射线DA,DB分别为x轴正半轴和y轴正半轴,建立如图的空间直角坐标系D-xyz,
则A(1,0,0),B(0,1,0),D(0,0,0).…(6分)

由(Ⅰ)可设点C的坐标为(x,1,z),其中z>0,
则有x2+z2=1. ①
因为△ABC为等腰三角形,
所以AC=1或AC=
| 2 |
若AC=1,则有(x-1)2+1+z2=1.
则此得x=1,z=0,不合题意.
若AC=
| 2 |
联立①和②得x=
| 1 |
| 2 |
| ||
| 2 |
因此点C的坐标为(
| 1 |
| 2 |
| ||
| 2 |
由于DA⊥BD,BC⊥BD,所以
| DA |
| BC |
∵
| DA |
| BC |
| 1 |
| 2 |
| ||
| 2 |
∴cos<
| DA |
| BC |
| ||||
|
|
| 1 |
| 2 |
所以<
| DA |
| BC |
点评:本题以一个平面翻折问题为载体,考查了空间的线面位置关系,考查了平面与平面垂直的判定和两个平面所成角的大小求法等知识,属于中档题.

练习册系列答案
相关题目
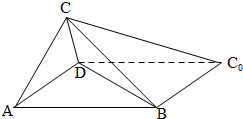 如图,一张平行四边形的硬纸片ABC0D中,AD=BD=1,
如图,一张平行四边形的硬纸片ABC0D中,AD=BD=1,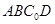 中,
中,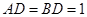 ,
, 。沿它的对角线
。沿它的对角线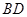 把△
把△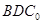 折起,使点
折起,使点 到达平面
到达平面 的位置。
的位置。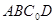 与平面
与平面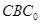 的位置关系,并给出证明;
的位置关系,并给出证明;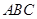 为等腰三角形,求此时二面角
为等腰三角形,求此时二面角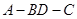 的大小。
的大小。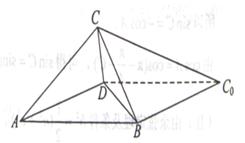
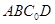 中,
中,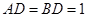 ,
,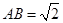 。沿它的对角线
。沿它的对角线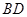 把△
把△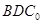 折起,使点
折起,使点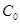 到达平面
到达平面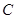 的位置。
的位置。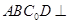 平面
平面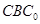 ;
;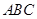 为等腰三角形,求二面角
为等腰三角形,求二面角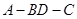 的大小。
的大小。