题目内容
一个直角三角形三边长a、b、c成等差数列,面积为12,则它的周长为
12
| 2 |
12
.| 2 |
分析:首先根据题意可知b一定不是斜边,设c为斜边,然后根据直角三角形、三边成等差数列、以及面积,列出式子,进而解出a、b、c,即可求出周长.
解答:解:由条件知b一定不是斜边,设c为斜边,
∵直角三角形三边长a、b、c成等差数列
∴2b=a+c ①
a2+b2=c2 ②
∵面积为12
∴
ab=12 ③
联立①②③,解得:b=4
,a=3
,c=5
∴a+b+c=12
故答案为:12
∵直角三角形三边长a、b、c成等差数列
∴2b=a+c ①
a2+b2=c2 ②
∵面积为12
∴
| 1 |
| 2 |
联立①②③,解得:b=4
| 2 |
| 2 |
| 2 |
∴a+b+c=12
| 2 |
故答案为:12
| 2 |
点评:此题考查了等差数列的性质、三角形的面积等知识,属于基础题.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案
相关题目
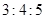 , B.三边边长之比为
, B.三边边长之比为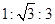 ,
,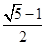 , D.较大锐角的正弦为
, D.较大锐角的正弦为