题目内容
10.已知函数y=(k-1)x2+(k2+3k-4)x+2是偶函数,求k的值.分析 由题意可得,k2+3k-4=0,从而可得答案.
解答 解:∵f(x)=(k-1)x2+(k2+3k-4)x+2是偶函数,
∴f(-x)=f(x),
∴2(k2+3k-4)x=0,而x不恒为0,
∴k2+3k-4=0,
∴k=1或k=-4.
故答案为:1或-4.
点评 本题考查函数奇偶性的性质,掌握奇偶函数的定义是解决问题之关键,属于基础题.

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目
20.已知直线l的倾斜角是120°,则这条直线的一个法向量为( )
| A. | (1,$\sqrt{3}$) | B. | (1,-$\sqrt{3}$) | C. | ($\sqrt{3}$,1) | D. | (-$\sqrt{3}$,1) |
18.已知点A(1,2),B(4,-2),则线段AB的长度为( )
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
5.一场通过网络发起的旨在倡导节约粮食的“光盘行动”引起热烈响应,1月23日,“光盘行动”微博转发超3000万次,若每天以30%的增速转发,则至1月25日将突破( )
| A. | 3900万次 | B. | 4800万次 | C. | 5070万次 | D. | 6591万次 |
15.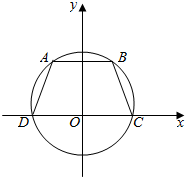 如图,已知等腰梯形ABCD的底边长分别为2和14,腰长为10,则这个等腰梯形的外接圆E的方程为( )
如图,已知等腰梯形ABCD的底边长分别为2和14,腰长为10,则这个等腰梯形的外接圆E的方程为( )
 如图,已知等腰梯形ABCD的底边长分别为2和14,腰长为10,则这个等腰梯形的外接圆E的方程为( )
如图,已知等腰梯形ABCD的底边长分别为2和14,腰长为10,则这个等腰梯形的外接圆E的方程为( )| A. | x2+(y-2)2=53 | B. | x2+(y-2)2=64 | C. | x2+(y-1)2=50 | D. | x2+(x-1)2=64 |