题目内容
19.若f(x)=$\left\{\begin{array}{l}{lo{g}_{2}x,0<x≤1}\\{\frac{{x}^{2}+2}{2x},x>1}\end{array}\right.$,若方程f(x)=k(x-1)有两个实根,则实数k的取值范围是($\frac{1}{2}$,$\frac{1}{ln2}$].分析 作函数图象,结合图象讨论,由分段函数分别求在各段上解的个数,从而综合讨论即可.
解答  解:∵方程f(x)=k(x-1)有两个实根,
解:∵方程f(x)=k(x-1)有两个实根,
∴函数f(x)=$\left\{\begin{array}{l}{lo{g}_{2}x,0<x≤1}\\{\frac{{x}^{2}+2}{2x},x>1}\end{array}\right.$与y=k(x-1)的图象有两个不同的交点,
作其图象如右图,
当x>1时,方程f(x)=k(x-1)可化为k=$\frac{{x}^{2}+2}{2x(x-1)}$,
令F(x)=$\frac{{x}^{2}+2}{2x(x-1)}$,则F′(x)=$\frac{{x}^{2}+2}{2x(x-1)}$=$\frac{1}{2}$•$\frac{-(x+2)^{2}+6}{{x}^{2}(x-1)^{2}}$<0,
∴F(x)在(1,+∞)上单调递减;
又∵$\underset{lim}{x→+∞}$$\frac{{x}^{2}+2}{2x(x-1)}$=$\frac{1}{2}$,
∴当k>$\frac{1}{2}$时,方程f(x)=k(x-1)在(1,+∞)上有一个解,
当k$≤\frac{1}{2}$时,方程f(x)=k(x-1)在(1,+∞)上无解;
当点(1,0)是y=log2x的切点时,y′=$\frac{1}{ln2}$;
故当k>$\frac{1}{ln2}$时,直线y=k(x-1)与y=log2x在(0,1]上有两个交点,
当k≤$\frac{1}{ln2}$时,直线y=k(x-1)与y=log2x在(0,1]上有一个交点(1,0),
结合讨论可知,
当k∈($\frac{1}{2}$,$\frac{1}{ln2}$]时,方程f(x)=k(x-1)有两个实根,
故答案为:($\frac{1}{2}$,$\frac{1}{ln2}$].
点评 本题考查了导数的综合应用及数形结合的思想应用,同时考查了分类讨论的思想.

| A. | a<c<b | B. | a<b<c | C. | b<a<c | D. | b<c<a |

 如图所示,在正四棱柱ABCD-A1B1C1D1中,E、F分别是AA1、CC1的中点,AB=AD=1,AA1=$\sqrt{2}$.
如图所示,在正四棱柱ABCD-A1B1C1D1中,E、F分别是AA1、CC1的中点,AB=AD=1,AA1=$\sqrt{2}$.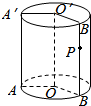 如图,圆柱OO′的底面半径为2cm,高为4cm,且P为母线B′B的重点,∠AOB=120°,则一蚂蚁从A点沿圆柱表面爬到P点的最短路程为$\frac{2}{3}\sqrt{4{π}^{2}+9}$.
如图,圆柱OO′的底面半径为2cm,高为4cm,且P为母线B′B的重点,∠AOB=120°,则一蚂蚁从A点沿圆柱表面爬到P点的最短路程为$\frac{2}{3}\sqrt{4{π}^{2}+9}$.