题目内容
求证：A（2，2），B（5，3），C（3，-1），D（6，0）四点共圆，并求出此圆的圆心和半径．
考点：圆的一般方程
专题：直线与圆
分析：首先由不共线三点确定一个圆，然后再证第四个点在圆上，用待定系数法．
解答：
解：设所共圆的方程为x2+y2+Dx+Ey+F=0．将A、B、D三点坐标代入得
，
解得D=-8，E=-2，F=12，
故过A、B、D三点的圆的方程为x2+y2-8x-2y+12=0．
把点C（3，-1）代入方程的左边=9+1-24+2+12=0．
∴点C在该圆上．∵-
=4，-
=1，
∴圆心为（4，1），r=
=
，
综上，可得四点共圆于圆心为（4，1），半径为
的圆，
其方程为x2+y2-8x-2y+12=0．
|
解得D=-8，E=-2，F=12，
故过A、B、D三点的圆的方程为x2+y2-8x-2y+12=0．
把点C（3，-1）代入方程的左边=9+1-24+2+12=0．
∴点C在该圆上．∵-
| D |
| 2 |
| E |
| 2 |
∴圆心为（4，1），r=
| ||
| 2 |
| 5 |
综上，可得四点共圆于圆心为（4，1），半径为
| 5 |
其方程为x2+y2-8x-2y+12=0．
点评：圆的标准方程中有三个未知量a，b，r；圆的一般方程有三个未知量D，E，F．故确定一个圆需要三个独立的条件，一般利用待定系数法确定．这需要把题目中的已知条件一一转化为关于未知量的方程，利用方程组获得a，b，r或D，E，F的值，进而确定圆的方程．
练习册系列答案
相关题目
如图，已知矩形ABCD，P为平面ABCD外一点，M、N分别为BC、PD的中点，且满足椭圆的焦点坐标为（4，0），（-4，0），椭圆上一点到两焦点的距离之和为10，则椭圆的标准方程为（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知圆M：（x+2）2+y2=4，过点P（-1，0）作圆M的互相垂直的两条弦AB，CD，则这两条弦长之和的最大值为（ ）
A、2
| ||
| B、8 | ||
C、4+2
| ||
D、4
|
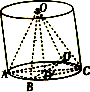在一个圆柱中挖去一个内接正四棱锥O-ABCD（顶点是上面底面积圆的圆心O，底面是下底面的内接正方形），得到如图所示的几何体，已知圆柱底面直径为4已知一个家庭有两个小孩，则两个孩子都是女孩的概率为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
如图，若输入n的值为4，则输出A的值为（ ）
| A、3 | ||
| B、-2 | ||
C、-
| ||
D、
|