题目内容
已知向量![]() , 向量
, 向量![]() , 且
, 且![]() , 动点
, 动点![]() 的轨迹为E.
的轨迹为E.
(1)求轨迹E的方程;
(2)证明:存在圆心在原点的圆,使得该圆的任意一条切线与轨迹E恒有两个交点A,B, 且![]() (O为坐标原点),并求出该圆的方程;
(O为坐标原点),并求出该圆的方程;
解:(1)因为![]() ,
,![]() ,
, ![]() ,
,
所以![]()
![]() , 所以,轨迹E的方程为:
, 所以,轨迹E的方程为:![]() . w ……… 4分
. w ……… 4分
(2).设圆心在原点的圆的一条切线为![]() ,解方程组
,解方程组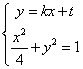 得
得![]() ,即
,即![]() , ………………… 6分
, ………………… 6分
要使切线与轨迹E恒有两个交点A,B,
则使△=![]() ,
,
即![]() ,即
,即![]() , 且
, 且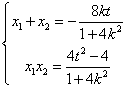
![]() ,
,
要使![]() , 需使
, 需使![]() ,即
,即![]() ,
,
所以![]() , 即
, 即![]() 且
且![]() , 即
, 即![]()
即![]() ,恒成立. ………………… 10分
,恒成立. ………………… 10分
又因为直线![]() 为圆心在原点的圆的一条切线,
为圆心在原点的圆的一条切线,
所以圆的半径为![]() ,
,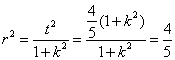 , 所求的圆为
, 所求的圆为![]() .
.
当切线的斜率不存在时,切线为![]() ,与
,与![]() 交于点
交于点![]() 或
或![]() 也满足
也满足![]() .
.
综上, 存在圆心在原点的圆![]() ,使得该圆的任意一条切线与椭圆E恒有两个交点A, B,
,使得该圆的任意一条切线与椭圆E恒有两个交点A, B,
且![]() . …………… 14分
. …………… 14分

练习册系列答案
 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目