题目内容
在平面直角坐标系xOy中,点A(5,0),对于某个正实数k,存在函数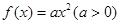 ,使得
,使得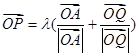 (
( 为常数),这里点P、Q的坐标分别为
为常数),这里点P、Q的坐标分别为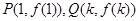 ,则k的取值范围为( )
,则k的取值范围为( )
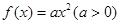 ,使得
,使得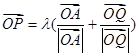 (
( 为常数),这里点P、Q的坐标分别为
为常数),这里点P、Q的坐标分别为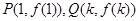 ,则k的取值范围为( )
,则k的取值范围为( )A.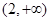 | B.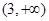 | C. | D. |
A
由题设知,向量
 ,
, ,
, ,
, ,
, ,由
,由 知
知 ,
, ,两式相除得,
,两式相除得, ,
,

 ,
,
故选A.
点评:本题考查平面向量的综合运算,解题时要认真审题,注意挖掘题设中的隐含条件,合理地进行等价转化.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
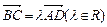 ,
,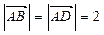 ,
,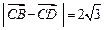 .
.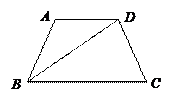
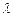 的值;
的值;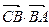 .
.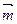 =(1,
=(1, 1),向量
1),向量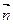 与向量
与向量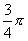 ,且
,且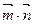 =-1.
=-1.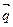 =(1,0)的夹角为
=(1,0)的夹角为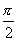 ,向量
,向量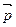 =
=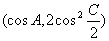 ,其中A、C
,其中A、C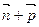 |的取值范围;
|的取值范围;
 则
则 的值等于
的值等于 -t
-t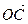 )·
)·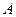 (5,7),
(5,7), (2,3),将
(2,3),将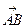 沿
沿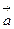 =(4,1)平移后的坐标为 ( )
=(4,1)平移后的坐标为 ( )  ,且
,且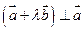 ,则实数
,则实数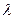 的值是( )
的值是( )
 |=
|= ,则
,则 =
=