题目内容
已知函数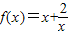 .
.(1)判断f(x)的奇偶性,并证明你的结论;
(2)证明:函数f(x)在
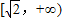 内是增函数.
内是增函数.
【答案】分析:(1)利用函数奇偶性的定义去判断.(2)利用函数单调性的定义去证明.
解答:解:(1)函数的定义域是(-∞,0)∪(0,+∞)(1分)
∵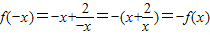 ,
,
∴f(x)是奇函数.(5分)
(2)设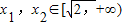 ,且x1<x2 (6分)
,且x1<x2 (6分)
则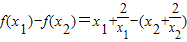 =
=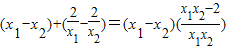 ,(7分)
,(7分)
∵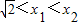 ,
,
∴x1-x2<0,x1x2-2>0,x1x2>0(10分)
∴f(x1)-f(x2)<0,即f(x1)<f(x2)(11分)
故f(x)在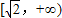 内是增函数.(12分)
内是增函数.(12分)
点评:本题主要考查函数奇偶性的判断和单调性的判断,利用函数单调性和奇偶性的定义是解决本题的关键.
解答:解:(1)函数的定义域是(-∞,0)∪(0,+∞)(1分)
∵
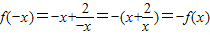 ,
,∴f(x)是奇函数.(5分)
(2)设
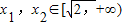 ,且x1<x2 (6分)
,且x1<x2 (6分)则
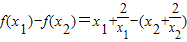 =
=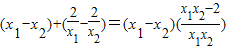 ,(7分)
,(7分)∵
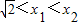 ,
,∴x1-x2<0,x1x2-2>0,x1x2>0(10分)
∴f(x1)-f(x2)<0,即f(x1)<f(x2)(11分)
故f(x)在
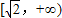 内是增函数.(12分)
内是增函数.(12分)点评:本题主要考查函数奇偶性的判断和单调性的判断,利用函数单调性和奇偶性的定义是解决本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目

 ,
, 上的单调性;
上的单调性; .
. ,求a,b的值.
,求a,b的值. .
. 的奇偶性;(4分)
的奇偶性;(4分) 的方程
的方程 有两解,求实数
有两解,求实数 的取值范围;(6分)
的取值范围;(6分) ,记
,记 ,试求函数
,试求函数 在区间
在区间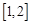 上的最大值.(10分)
上的最大值.(10分) .
. ,
, 的奇偶性;(2)求证:方程
的奇偶性;(2)求证:方程 至少有一根在区间
至少有一根在区间