题目内容
设数列{an} 为等差数列,且a5=14,a7=20,数列{bn} 的前n项和为Sn=1﹣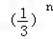 (n∈
(n∈
N*),
(Ⅰ)求数列{an},{bn}的通项公式;
(Ⅱ)若cn=anbn,n=1,2,3,…,求数列{cn}的前n项和Tn.
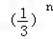 (n∈
(n∈N*),
(Ⅰ)求数列{an},{bn}的通项公式;
(Ⅱ)若cn=anbn,n=1,2,3,…,求数列{cn}的前n项和Tn.
(Ⅰ)解:∵数列{an}为等差数列,且a5=14,a7=20,
∴公差d=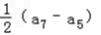 =3,
=3,
∵a5=a1+4×3=14,
∴a1=2. ∴an=2+(n﹣1)×3=3n﹣1.
∵数列{bn}的前n项和为Sn=1﹣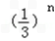 (n∈N*),
(n∈N*),
∴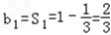 , bn=Sn﹣Sn﹣1=[1﹣
, bn=Sn﹣Sn﹣1=[1﹣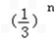 ]﹣[1﹣
]﹣[1﹣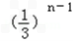 ]=
]= 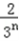 ,
,
当n=1时,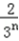 =
= 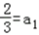 , ∴
, ∴ 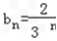 .
.
(Ⅱ)由an=3n﹣1,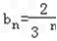 ,得cn=an·bn=
,得cn=an·bn=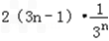 ,
,
∴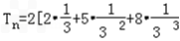
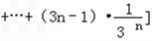 ,
,
 Tn=
Tn=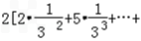
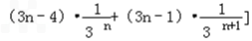 ,
,
两式相减,得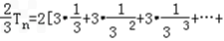
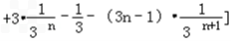 ,
,
∴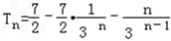 .
.
∴公差d=
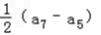 =3,
=3,∵a5=a1+4×3=14,
∴a1=2. ∴an=2+(n﹣1)×3=3n﹣1.
∵数列{bn}的前n项和为Sn=1﹣
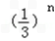 (n∈N*),
(n∈N*),∴
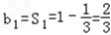 , bn=Sn﹣Sn﹣1=[1﹣
, bn=Sn﹣Sn﹣1=[1﹣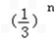 ]﹣[1﹣
]﹣[1﹣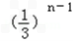 ]=
]= 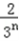 ,
,当n=1时,
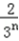 =
= 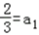 , ∴
, ∴ 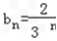 .
.(Ⅱ)由an=3n﹣1,
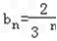 ,得cn=an·bn=
,得cn=an·bn=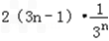 ,
, ∴
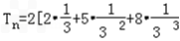
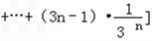 ,
,  Tn=
Tn=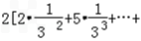
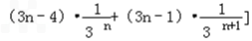 ,
,两式相减,得
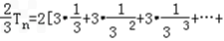
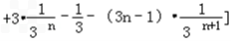 ,
, ∴
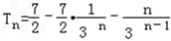 .
. 
练习册系列答案
 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目
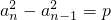 (p为常数,n≥2,n∈N*),则称数列{an}为等方差数列,p为公方差,已知正数等方差数列{an}的首项a1=1,且a1,a2,a5成等比数列,a1≠a2,设集合
(p为常数,n≥2,n∈N*),则称数列{an}为等方差数列,p为公方差,已知正数等方差数列{an}的首项a1=1,且a1,a2,a5成等比数列,a1≠a2,设集合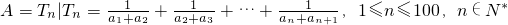 ,取A的非空子集B,若B的元素都是整数,则B为“完美子集”,那么集合A中的完美子集的个数为
,取A的非空子集B,若B的元素都是整数,则B为“完美子集”,那么集合A中的完美子集的个数为