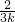Question

设双曲线2x²-3y²=6的一条弦AB被直线y=kx平分，则AB所在直线的斜率为（　　）

• A、

  2

  3k

• B、

  6

  3k

• C、

  5

  3

  k
• D、

  6

  2

  k

Answer 1

分析：设AB的斜率为k′，A（x₁，y₁）B（x₂，y₂），中点坐标（x₀，y₀）把A，B代入双曲线方程两式想减整理可得

x0

y0

=

3

2

k′，根据AB的中点在直线y=kx上，代入得y₀=kx₀，进而求得k和k′的关系．

解答：解：设AB的斜率为k′，
则A（x₁，y₁）B（x₂，y₂），中点坐标（x₀，y₀）
x₀=

x1+x2

2

，y₀=

y1+y2

2

由题意：2x₁²-3y₁²=6，2x₂²-3y₂²=6
两式相减，整理得
2（x₁+x₂）（x₁-x₂）=3（y₁+y₂）（y₁-y₂）
∴

x1+x2

y1+y2

=

3(y2-y2)

2(x1-x2)

即

x0

y0

=

3

2

k′
∵AB的中点在直线y=kx上，代入得y₀=kx₀，
∴

x0

y0

=k
∴k′=

2

3

k
故选A

点评：本题主要考查了直线与圆锥曲线的综合问题．涉及了直线的斜率问题，直线方程问题，考查了学生对所学知识综合性的把握．