题目内容
实数a为何值时,圆x2+y2-2ax+a2-1=0与抛物线y2=
x有两个公共点.
| 1 | 2 |
分析:利用圆x2+y2-2ax+a2-1=0与抛物线y2=
x有两个公共点,联立方程,根据根的判别式,结合图象的变换,即可求a的值.
| 1 |
| 2 |
解答:解:由x2+y2-2ax+a2-1=0,可得标准方程为:(x-a)2+y2=1
由此可知,这是一个圆心在(a,0),半径恒为1的圆;参数a只影响圆心的位置,与半径大小无关.
当a=0时,该圆变成圆心在原点,半径为1的单位圆:x2+y2=1,其与抛物线y2=
x当然会有两个交点.
将抛物线y2=
x代入圆的方程,得:x2+(
-2a)x+a2-1=0…(1)
令其判别式△=(
-2a)2-4(a2-1)=0,得a=
,此时圆与抛物线有两个公共点;
将圆心在x轴上向左移动到a=-1时,圆的方程变为(x+1)2+y2-1=x2+y2+2x=0
将y2=
x代入得x(x+
)=0,可知圆与抛物线有唯一的一个交点x=0,(x=-
舍去,因为x=-
不在抛物线的定义域内).
综上,当-1<a≤
时,圆x2+y2-2ax+a2-1-0与抛物线y2=
x有两个公共点.
由此可知,这是一个圆心在(a,0),半径恒为1的圆;参数a只影响圆心的位置,与半径大小无关.
当a=0时,该圆变成圆心在原点,半径为1的单位圆:x2+y2=1,其与抛物线y2=
| 1 |
| 2 |
将抛物线y2=
| 1 |
| 2 |
| 1 |
| 2 |
令其判别式△=(
| 1 |
| 2 |
| 17 |
| 8 |
将圆心在x轴上向左移动到a=-1时,圆的方程变为(x+1)2+y2-1=x2+y2+2x=0
将y2=
| 1 |
| 2 |
| 9 |
| 4 |
| 9 |
| 4 |
| 9 |
| 4 |
综上,当-1<a≤
| 17 |
| 8 |
| 1 |
| 2 |
点评:本题考查圆与抛物线的位置关系,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
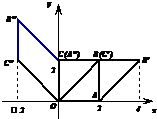 (Ⅰ)如图,正方形OABC在二阶矩阵M对应的切变变换作用下变为平行四边形OA′B′C′,平行四边形OA'B'C'在二阶矩阵N对应的旋转变换作用下变为平行四边形OA''B''C'',求将正方形OABC变为平行四边形OA''B''C''的变换对应的矩阵.
(Ⅰ)如图,正方形OABC在二阶矩阵M对应的切变变换作用下变为平行四边形OA′B′C′,平行四边形OA'B'C'在二阶矩阵N对应的旋转变换作用下变为平行四边形OA''B''C'',求将正方形OABC变为平行四边形OA''B''C''的变换对应的矩阵.