题目内容
如图所示的三角形数阵叫“莱布尼兹调和三角形”,它们是由整数的倒数组成的,第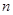 行有
行有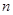 个数且两端的数均为
个数且两端的数均为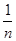
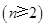 ,每个数是它下一行左右相邻两数的和,如
,每个数是它下一行左右相邻两数的和,如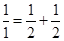 ,
,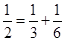 ,
,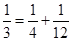 , ,则第7行第4个数(从左往右数)为( )
, ,则第7行第4个数(从左往右数)为( )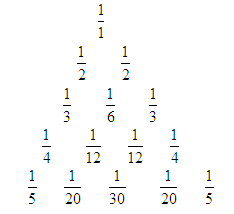
A.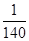 | B.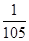 | C.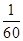 | D.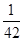 |
A
解析试题分析:根据每个数是它下一行左右相邻两数的和,先求出第5,6,7三行的第2个数,再求出6,7两行的第3个数,求出第7行的第4个数.解:设第n行第m个数为a(n,m),由题意知a(6,1)= ,a(7,1)=
,a(7,1)= ∴a(7,2)=a(6,1)-a(7,1)=
∴a(7,2)=a(6,1)-a(7,1)= -
- =
=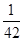 , a(6,2)=a(5,1)-a(6,1)=
, a(6,2)=a(5,1)-a(6,1)=
 =
= , a(7,3)=a(6,2)-a(7,2)=
, a(7,3)=a(6,2)-a(7,2)= -
-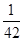
=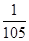 , a(6,3)=a(5,2)-a(6,2)=
, a(6,3)=a(5,2)-a(6,2)= =
=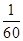 -∴a(7,4)=a(6,3)-a(7,3)=
-∴a(7,4)=a(6,3)-a(7,3)=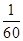 -
-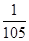 =
=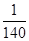 .故选A
.故选A
考点:归纳猜想
点评:本题考查通过观察归纳出各数的关系,考差了学生的观察能力和计算能力,属于中档题,解题时要认真审题,仔细解答,避免错误

练习册系列答案
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案
相关题目
各项均为正数的数列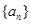 ,
,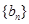 满足:
满足: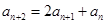 ,
,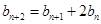 ,
,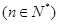 ,那么( )
,那么( )
A.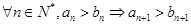 | B.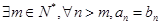 |
C.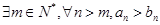 | D. |
已知数列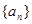 中,
中,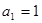 ,2
,2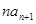 =
=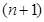
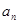 ,则数列
,则数列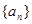 的通项公式为( )
的通项公式为( )
A.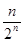 | B.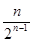 | C.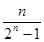 | D.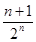 |
若数列 满足
满足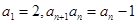 ,则
,则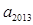 的值为
的值为
A.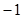 | B.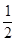 | C.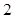 | D.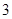 |
已知数列 为等差数列,
为等差数列,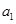 +
+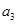 +
+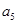
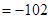 ,
,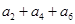
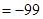 ,以
,以 表示
表示 的前
的前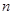 项和,则使得
项和,则使得 达到最小值的
达到最小值的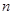 是( )
是( )
| A.37和38 | B.38 | C.37 | D.36和37 |
已知数列 满足
满足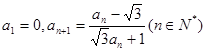 ,则
,则 等于( )
等于( )
A.0 | B.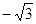 | C.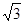 | D. |
已知数列 成等差数列,
成等差数列,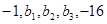 成等比数列,则
成等比数列,则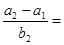 ( )
( )
A.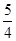 | B.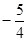 | C.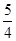 或 或 | D. |
已知数列 满足:
满足: ,
, ,当且仅当
,当且仅当 时
时 最小,则实数
最小,则实数 的取值范围是( )
的取值范围是( )
A. | B. | C.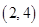 | D. |
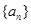 满足条件
满足条件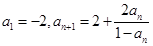 , 则
, 则 = ;
= ;