题目内容
已知数列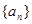 中,
中,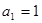 ,2
,2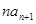 =
=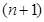
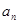 ,则数列
,则数列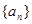 的通项公式为( )
的通项公式为( )
A.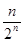 | B.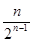 | C.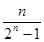 | D.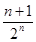 |
B
解析试题分析:已知条件可化为 ,这种递推公式的数列求通项的话,一般用累乘的方法.
,这种递推公式的数列求通项的话,一般用累乘的方法.
∴ .选B.
.选B.
考点:数列的递推公式.

练习册系列答案
相关题目
已知数列 满足
满足 则
则 等于( )
等于( )
| A.2 | B. | C.-3 | D. |
已知数列 的前n项和为
的前n项和为 ,且
,且 ,则
,则 等于( )
等于( )
| A.4 | B.2 | C.1 | D.-2 |
已知数列 的通项公式
的通项公式 ,则数列的前
,则数列的前 项和
项和 的最小值是( )
的最小值是( )
A.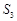 | B. | C.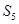 | D. |
若数列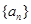 满足
满足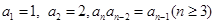 ,则
,则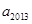 的值为 ( )
的值为 ( )
| A.2 | B. | C.1 | D. |
函数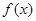 由右表定义:若
由右表定义:若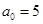 ,
,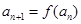 ,
,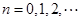 ,则
,则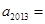 ( )
( )
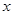 |  | 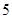 | 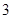 | 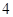 |
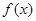 |  | 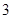 | 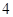 | 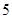 |
如图所示的三角形数阵叫“莱布尼兹调和三角形”,它们是由整数的倒数组成的,第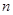 行有
行有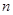 个数且两端的数均为
个数且两端的数均为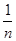
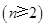 ,每个数是它下一行左右相邻两数的和,如
,每个数是它下一行左右相邻两数的和,如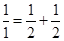 ,
,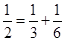 ,
,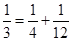 , ,则第7行第4个数(从左往右数)为( )
, ,则第7行第4个数(从左往右数)为( )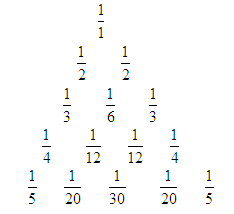
A.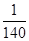 | B.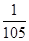 | C.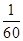 | D.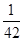 |
实数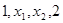 成等差数列,
成等差数列,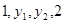 成等比数列,则
成等比数列,则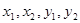 的大小关系是( )
的大小关系是( )
A.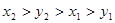 | B.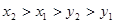 |
C.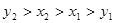 | D.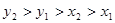 |
数列{an}的前n项和为Sn=4n2-n+2,则该数列的通项公式为( )
| A.an=8n-5(n∈N*) |
B.an= |
| C.an=8n+5(n≥2) |
| D.an=8n+5(n≥1) |