题目内容
 如图,F1、F2是椭圆C1:
如图,F1、F2是椭圆C1:| x2 |
| a2 |
| y2 |
| b2 |
分析:由于AF2⊥x轴,可得A(c,
).由于△F1AB为等腰直角三角形,可得|F1F2|=|AF2|,于是2c=
,再利用b2=a2-c2,e=
即可得出.
| b2 |
| a |
| b2 |
| a |
| c |
| a |
解答:解:∵AF2⊥x轴,∴A(c,
).
∵△F1AB为等腰直角三角形,∴|F1F2|=|AF2|,
∴2c=
,∴2ac=b2=a2-c2,
∴2e=1-e2,
化为e2+2e-1=0,(e>0).
解得e=
=
-1.
故选:A.
| b2 |
| a |
∵△F1AB为等腰直角三角形,∴|F1F2|=|AF2|,
∴2c=
| b2 |
| a |
∴2e=1-e2,
化为e2+2e-1=0,(e>0).
解得e=
-2+2
| ||
| 2 |
| 2 |
故选:A.
点评:本题考查了椭圆的坐标方程及其性质、等腰直角三角形等基础知识与基本技能方法,属于基础题.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
 (2013•浦东新区二模)(1)设椭圆C1:
(2013•浦东新区二模)(1)设椭圆C1: 如图,F1,F2为椭圆C:
如图,F1,F2为椭圆C: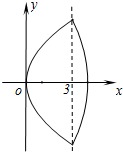 (1)设椭圆C1:
(1)设椭圆C1: 与双曲线C2:
与双曲线C2: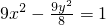 有相同的焦点F1、F2,M是椭圆C1与双曲线C2的公共点,且△MF1F2的周长为6,求椭圆C1的方程;
有相同的焦点F1、F2,M是椭圆C1与双曲线C2的公共点,且△MF1F2的周长为6,求椭圆C1的方程;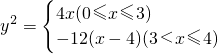 .设“盾圆D”上的任意一点M到F(1,0)的距离为d1,M到直线l:x=3的距离为d2,求证:d1+d2为定值;
.设“盾圆D”上的任意一点M到F(1,0)的距离为d1,M到直线l:x=3的距离为d2,求证:d1+d2为定值; 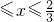 )与第(1)小题椭圆弧E2:
)与第(1)小题椭圆弧E2: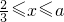 )所合成的封闭曲线为“盾圆E”.设过点F(1,0)的直线与“盾圆E”交于A、B两点,|FA|=r1,|FB|=r2且∠AFx=α(0≤α≤π),试用cosα表示r1;并求
)所合成的封闭曲线为“盾圆E”.设过点F(1,0)的直线与“盾圆E”交于A、B两点,|FA|=r1,|FB|=r2且∠AFx=α(0≤α≤π),试用cosα表示r1;并求 的取值范围.
的取值范围.