题目内容
已知sinφ·cosφ=
解:方法一:∵sinφcosφ=![]() ,
,
∴sin2φ=![]() .
.
又∵![]() <φ<
<φ<![]() ,
,![]() <2φ<π,cos2φ<0,
<2φ<π,cos2φ<0,
∴cos2φ=![]() ,sinφ>0,cosφ>0.
,sinφ>0,cosφ>0.
∴sinφ=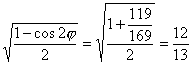 ,
,
cosφ=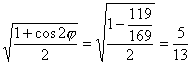 .
.
方法二:(sinφ+cosφ)2=1+2sinφcosφ=1+![]() =
=![]() ,
,
∵![]() <φ<
<φ<![]() ,sinφ>0,cosφ>0.
,sinφ>0,cosφ>0.
∴sinφ+cosφ=![]() .①
.①
又(sinφ-cosφ)2=1-2sinφcosφ=1-![]() =
=![]() ,
,
∵![]() <φ<
<φ<![]() ,则sinφ>cosφ>0,
,则sinφ>cosφ>0,
∴sinφ-cosφ>0,sinφ-cosφ=![]() .②
.②
解①②的方程组得sinφ=![]() ,cosφ=
,cosφ=![]() .
.

练习册系列答案
相关题目