题目内容
7．讨论函数y=loga|x-2|的单调性．分析 令t=|x-2|=$\left\{\begin{array}{l}-x+2，x＜2\\ x-2，x＞2\end{array}\right.$，则内函数在（-∞，2）上为减函数，在（2，+∞）上为增函数，分类讨论外函数的单调性，结合复合函数“同增异减”的原则，可得复合函数的单调性．
解答 解：由|x-2|＞0得：x∈（-∞，2）∪（2，+∞），
令t=|x-2|=$\left\{\begin{array}{l}-x+2，x＜2\\ x-2，x＞2\end{array}\right.$，
则y=logat，
当0＜a＜1时，y=logat为减函数，
t=$\left\{\begin{array}{l}-x+2，x＜2\\ x-2，x＞2\end{array}\right.$在（-∞，2）上为减函数，在（2，+∞）上为增函数，
故函数y=loga|x-2|在（-∞，2）上为增函数，在（2，+∞）上为减函数，
当a＞1时，y=logat为增函数，
t=$\left\{\begin{array}{l}-x+2，x＜2\\ x-2，x＞2\end{array}\right.$在（-∞，2）上为减函数，在（2，+∞）上为增函数，
故函数y=loga|x-2|在（-∞，2）上为减函数，在（2，+∞）上为增函数．
点评 本题考查的知识点是复合函数的单调性，对数函数的图象和性质，难度中档．
练习册系列答案
相关题目
18．己知函数f（x）与它的导函数f'（x）满足x2f'（x）+xf（x）=lnx，且f（e）=$\frac{1}{e}$，则下列结论正确的是（ ）
| A． | f（x）在区间（0，+∞）上是减函数 | B． | f（x）在区间（0，+∞）上是增函数 | ||
| C． | f（x）在区间（0，+∞）上先增后减 | D． | f（x）在区间（0，+∞）上是先减后增 |
在三棱锥P-ABC中，PA⊥面ABC，∠ABC=90°，若AD⊥PB，垂足为D，求证：AD⊥面BPC．
2．设f（x）是奇函数，且f′（0）存在，则x=0是F（x）=$\frac{f（x）}{x}$的（ ）
| A． | 无穷间断点 | B． | 可去间断点 | C． | 连续点 | D． | 震荡间断点 |
12．
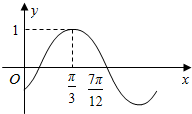已知函数y=Asin（ωx+φ）（ω＞0，|φ|＜$\frac{π}{2}$）的部分图象如图所示，则 （ ）
已知函数y=Asin（ωx+φ）（ω＞0，|φ|＜$\frac{π}{2}$）的部分图象如图所示，则 （ ）| A． | ω=1，φ=$\frac{π}{6}$ | B． | ω=1，φ=-$\frac{π}{6}$ | C． | ω=2，φ=$\frac{π}{6}$ | D． | ω=2，φ=-$\frac{π}{6}$ |