题目内容
已知a>0,函数f(x)=x3-a,x∈(0,+∞).设x1>0,记曲线y=f(x)在点(x1,f(x1))处的切线为l.(1)求l的方程.
(2)设l与x轴的交点为(x2,0),证明①x2≥![]() ;②若x1>
;②若x1>![]() ,则
,则![]() <x2<x1.
<x2<x1.
思路分析:利用导数的几何意义及证明不等式的基本方法求解.
(1)解:f′(x)=3x2,由此得切线l的方程为y-(x13-a)=3x12(x-x1).
(2)证明:依题意,切线方程中令y=0,x2=x1-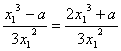 .
.
①x2-![]() =
=![]() (2x13+a-3x12
(2x13+a-3x12![]() )=
)=![]() (x1-
(x1-![]() )(2x12+
)(2x12+![]() x1-
x1-![]() )≥0,
)≥0,
∴x2≥![]() ,当且仅当x1=
,当且仅当x1=![]() 时等号成立.
时等号成立.
说明:当0<x1<![]() 时,x1-
时,x1-![]() <0,2x12-
<0,2x12-![]() x1-
x1-![]() <0,∴x2-
<0,∴x2-![]() >0;
>0;
当x1>![]() 时,x1-
时,x1-![]() >0,2x12-
>0,2x12-![]() x1-
x1-![]() >0,∴x2-
>0,∴x2-![]() >0;
>0;
当x1=![]() 时,x1-
时,x1-![]() =0,2x12-
=0,2x12-![]() x1-
x1-![]() =0,∴x2-
=0,∴x2-![]() =0.综上所述,当x1>0时,x2≥
=0.综上所述,当x1>0时,x2≥![]() .
.
②若x1>![]() ,则x13-a>0,x2-x1=
,则x13-a>0,x2-x1=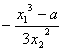 <0,且由①知当x1>
<0,且由①知当x1>![]() 时,x2>
时,x2>![]() ,
,
∴![]() <x2<x1.
<x2<x1.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
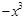 +ax在[1,+∞)上是减函数,则a的取值范围是(
)
+ax在[1,+∞)上是减函数,则a的取值范围是(
)