题目内容
已知a>0,函数f(x)=ax-bx2.(1)当b>0时,若对任意x∈R都有f(x)≤1,证明a≤![]() ;
;
(2)当0<b≤1时,讨论:对任意x∈[0,1],|f(x)|≤1的充要条件.
(1)证明:依题设,对任意x∈R,都有f(x)≤1,
∵f(x)=-b(x-![]() )2+
)2+![]() ,
,
∴f(![]() )=
)=![]() ≤1.
≤1.
∵a>0,b>0,∴a≤![]() .
.
(2)解析:因为a>0,0<b≤1时,对任意x∈[0,1],
f(x)=ax-bx2≥-b≥-1,即f(x)≥-1;
f(x)≤1![]() f(1)≤1
f(1)≤1![]() a-b≤1,即a≤b+1,
a-b≤1,即a≤b+1,
a≤b+1![]() f(x)≤(b+1)x-bx2≤1,即f(x)≤1.
f(x)≤(b+1)x-bx2≤1,即f(x)≤1.
所以,当a>0,0<b≤1时,对任意x∈[0,1],|f(x)|≤1的充要条件是a≤b+1.

练习册系列答案
相关题目
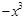 +ax在[1,+∞)上是减函数,则a的取值范围是(
)
+ax在[1,+∞)上是减函数,则a的取值范围是(
)