Question

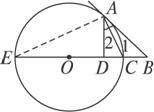
如图2-4-4,AD是⊙O的切线,AC是⊙O的弦,过C作AD的垂线,垂足为B,CB与⊙O相交于点E,AE平分∠CAB,且AE =2,求△ABC各边的长.

图2-4-4

Answer 1

思路解析:∠BAE为弦切角,于是∠BAE=∠C,再由AE平分∠CAB和△ABC是直角三角形可得∠C的度数,进而解直角三角形即可.

解:∵AD为⊙O的切线,?

∴∠BAE=∠C.?

∵AE平分∠CAB,?

∴∠BAC=2∠BAE.?

又∵∠C+∠BAC =90°,?

∴∠BAE =∠C =30°.?

则有BE =1,AB =,BC =3,AC =2.