题目内容
如图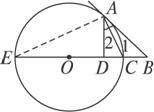
图
证明:连结AE,∵CE是直径,
∴∠CAE=90°.
∴∠E+∠ACE=90°.
∵AD⊥EC,∴∠ADC=90°.
∴∠2+∠ACE=90°.
∴∠2=∠E.
又∵AB切⊙O于A,AC是弦,
∴∠1=∠E.∴∠1=∠2.

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目
题目内容
如图
图
证明:连结AE,∵CE是直径,
∴∠CAE=90°.
∴∠E+∠ACE=90°.
∵AD⊥EC,∴∠ADC=90°.
∴∠2+∠ACE=90°.
∴∠2=∠E.
又∵AB切⊙O于A,AC是弦,
∴∠1=∠E.∴∠1=∠2.

 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案