题目内容
16.已知a、b、c∈R+,且a+b+c=1,求($\frac{1}{a}$-1)($\frac{1}{b}$-1)($\frac{1}{c}$-1)的最小值.分析 将条件代入,利用基本不等式,即可得出结论.
解答 解:∵a+b+c=1,a、b、c∈R+,
∴($\frac{1}{a}$-1)($\frac{1}{b}$-1)($\frac{1}{c}$-1)=$\frac{b+c}{a}•\frac{a+c}{b}•\frac{a+b}{c}$≥8,
当且仅当a=b=c时,($\frac{1}{a}$-1)($\frac{1}{b}$-1)($\frac{1}{c}$-1)的最小值为8.
点评 本题考查求最小值,考查基本不等式的运用,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
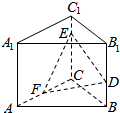 如图,已知正三棱柱ABC-A1B1C1中,AA1=4,AB=6,点D,E,F分别在棱BB1,CC1,AF上,且BD=C1E=$\frac{1}{2}$AF=1.
如图,已知正三棱柱ABC-A1B1C1中,AA1=4,AB=6,点D,E,F分别在棱BB1,CC1,AF上,且BD=C1E=$\frac{1}{2}$AF=1.