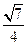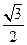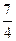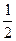题目内容
(本小题满分13分)已知椭圆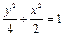 两焦点分别为
两焦点分别为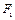 、
、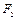 ,
,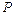 是椭圆在第一象限弧上的一点,并满足
是椭圆在第一象限弧上的一点,并满足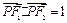 ,过点
,过点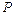 作倾斜角互补的两条直线
作倾斜角互补的两条直线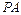 、
、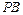 分别交椭圆于A、B两点.
分别交椭圆于A、B两点.
(1)求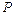 点坐标;
点坐标;
(2)证明:直线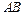 的斜率为定值,并求出该定值.
的斜率为定值,并求出该定值.
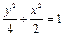 两焦点分别为
两焦点分别为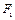 、
、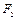 ,
,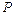 是椭圆在第一象限弧上的一点,并满足
是椭圆在第一象限弧上的一点,并满足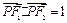 ,过点
,过点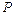 作倾斜角互补的两条直线
作倾斜角互补的两条直线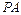 、
、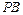 分别交椭圆于A、B两点.
分别交椭圆于A、B两点.(1)求
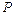 点坐标;
点坐标;(2)证明:直线
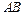 的斜率为定值,并求出该定值.
的斜率为定值,并求出该定值.(1)点P的坐标为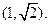
(2)直线AB斜率为定值,值为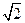 .
.
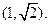
(2)直线AB斜率为定值,值为
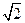 .
.解(1)由题可得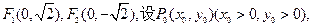
则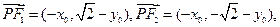 ①
①
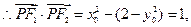
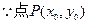 在曲线上,则
在曲线上,则 ②
②
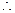 由①②得
由①②得 ,则点P的坐标为
,则点P的坐标为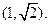 ……………(5分)
……………(5分)
(2)设直线PA斜率K,则直线PB斜率-K,设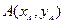 ,
,
则直线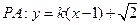 与椭圆方程联立得:
与椭圆方程联立得:
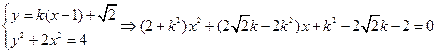
由韦达定理: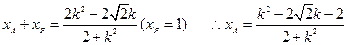
同理求得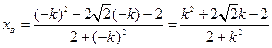
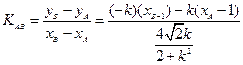
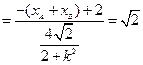
综上,直线AB斜率为定值,值为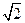 . …………(13分)
. …………(13分)
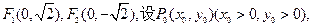
则
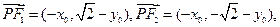 ①
①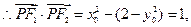
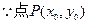 在曲线上,则
在曲线上,则 ②
②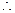 由①②得
由①②得 ,则点P的坐标为
,则点P的坐标为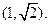 ……………(5分)
……………(5分)(2)设直线PA斜率K,则直线PB斜率-K,设
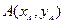 ,
,则直线
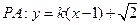 与椭圆方程联立得:
与椭圆方程联立得: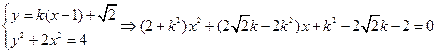
由韦达定理:
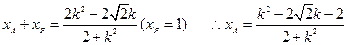
同理求得
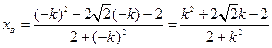
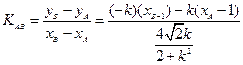
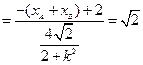
综上,直线AB斜率为定值,值为
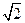 . …………(13分)
. …………(13分)
练习册系列答案
相关题目
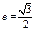 且椭圆经过
且椭圆经过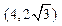 .
.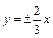 ,经过点
,经过点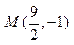 .
.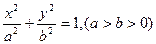 的左焦点,A(-a,0), B(0,b), 椭圆的离心率为
的左焦点,A(-a,0), B(0,b), 椭圆的离心率为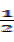 , 点D在x轴上,
, 点D在x轴上,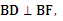 B,D,F三点确定的圆M恰好与直线l1:x+
B,D,F三点确定的圆M恰好与直线l1:x+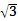 y+30相切
y+30相切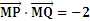 ,求直线l2的方程
,求直线l2的方程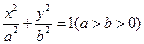 的离心率为
的离心率为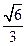 ,短轴的一个端点到右焦点的距离为
,短轴的一个端点到右焦点的距离为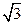 ,直线
,直线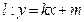 交椭圆于不同的两点
交椭圆于不同的两点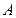 ,
,
 到直线
到直线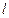 的距离为
的距离为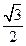 ,求
,求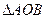 面积的最大值
面积的最大值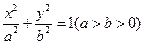 ,两个焦点分别为
,两个焦点分别为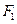 、
、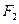 ,斜率为k的直线
,斜率为k的直线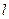 过右焦点
过右焦点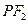 的中点恰为B。
的中点恰为B。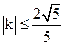 ,求椭圆C的离心率的取值范围。
,求椭圆C的离心率的取值范围。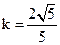 ,A、B到右准线距离之和为
,A、B到右准线距离之和为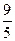 ,求椭圆C的方程。
,求椭圆C的方程。 题满分12分)如图所示,已知A、B、C是椭圆
题满分12分)如图所示,已知A、B、C是椭圆 上三点,其中点A的坐标为
上三点,其中点A的坐标为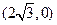 ,BC过椭圆的中心O,且
,BC过椭圆的中心O,且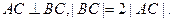
 Q,使得
Q,使得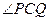 的平分线总垂直于z轴,试判断向量
的平分线总垂直于z轴,试判断向量 是否共线,并给出证明.
是否共线,并给出证明.
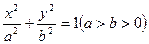 的右焦点为F,C为椭圆短轴的端点,向量
的右焦点为F,C为椭圆短轴的端点,向量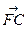 绕F点顺时针旋转
绕F点顺时针旋转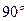 后得到向量
后得到向量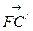 ,其中
,其中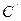 点恰好落在直线
点恰好落在直线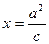 上,则该椭圆的离心率为__________________________
上,则该椭圆的离心率为__________________________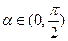 ,方程
,方程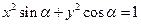 表示焦点在
表示焦点在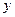 轴上的椭圆,则
轴上的椭圆,则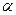 的取值范围是()
的取值范围是()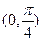
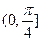
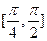
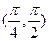
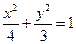 的离心率为
的离心率为