题目内容
12．在四边形ABCD中，已知顶点A（3，-2），B（-1，4），C（-2，-2），D（0，-5），求证：四边形ABCD是梯形．分析 由已知可得：$\overrightarrow{AB}=2\overrightarrow{DC}$，即可证明四边形ABCD是梯形．
解答 证明：∵$\overrightarrow{AB}$=（-1，4）-（3，-2）=（-4，6），
$\overrightarrow{DC}$=（-2，-2）-（0，-5）=（-2，3），
∴$\overrightarrow{AB}=2\overrightarrow{DC}$，
∴四边形ABCD是梯形．
点评 本题考查了向量坐标运算、向量共线与梯形的关系，考查了推理能力与计算能力，属于基础题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
2．等差数列{an}的前三项依次为a-1，a+1，2a+3，则此数列的第n项an=（ ）
| A． | 2n-5 | B． | 2n-3 | C． | 2n-1 | D． | 2n+1 |
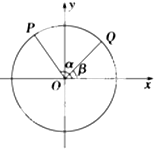如图，以Ox为始边作角α与β（0＜β＜α＜π），它们的终边分别与单位圆相交于P，Q两点，已知点P的坐标为$（{-\frac{3}{5}，\frac{4}{5}}）$