题目内容
4.设i是虚数单位,则复数z=$\frac{1-3{i}^{3}}{1-2i}$的共轭复数z在复平面内对应的点位于( )| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
分析 化简z,求出$\overline{z}$,从而求出其在复平面内对应的点所在的象限.
解答 解:z=$\frac{1-3{i}^{3}}{1-2i}$=$\frac{(1+3i)(1+2i)}{(1-2i)(1+2i)}$=$\frac{-5+5i}{5}$=-1+i,
故$\overline{z}$=-1-i,其在复平面内对应的点位于第三象限,
故选:C.
点评 本题考查了复数的运算,考查共轭复数问题,是一道基础题.

练习册系列答案
 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案
相关题目
12.方程x2+y2cosα=1(α∈R)不能表示的曲线为( )
| A. | 椭圆 | B. | 双曲线 | C. | 抛物线 | D. | 圆 |
19.设Sn为等比数列{an}的前n项和,且8a2+a5=0,则S3:S2的值为( )
| A. | -3 | B. | 5 | C. | -8 | D. | -11 |
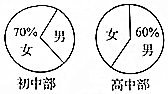 某中学初中部共有110名教师,高中部共有150名教师,其性别比例如图所示,则该校女教师的人数为137.
某中学初中部共有110名教师,高中部共有150名教师,其性别比例如图所示,则该校女教师的人数为137.