题目内容
=________．
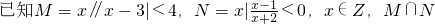{0}
分析：解含有绝对值的不等式|x-3|＜4，得到集合M={x|-1＜x＜7}；解分式不等式
，得集合N={x|-2＜x＜1且x∈Z}={-1，0}．最后根据交集的定义，可得M∩N={0}．
解答：∵|x-3|＜4
∴-4＜x-3＜4?-1＜x＜7
所以集合M={x||x-3|＜4}={x|-1＜x＜7}
∵
∴-2＜x＜1
所以集合N={x|，x∈Z}={x|-2＜x＜1且x∈Z}={-1，0}
∴集合M∩N={0}
故答案为：{0}
点评：本题以集合的交集运算为载体，着重考查了绝对值不等式和分式不等式的解法，属于基础题．
分析：解含有绝对值的不等式|x-3|＜4，得到集合M={x|-1＜x＜7}；解分式不等式
，得集合N={x|-2＜x＜1且x∈Z}={-1，0}．最后根据交集的定义，可得M∩N={0}．解答：∵|x-3|＜4
∴-4＜x-3＜4?-1＜x＜7
所以集合M={x||x-3|＜4}={x|-1＜x＜7}
∵
∴-2＜x＜1
所以集合N={x|
，x∈Z}={x|-2＜x＜1且x∈Z}={-1，0}∴集合M∩N={0}
故答案为：{0}
点评：本题以集合的交集运算为载体，着重考查了绝对值不等式和分式不等式的解法，属于基础题．
练习册系列答案
相关题目
=
，则角C的值为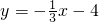
垂直的曲线C的切线方程为
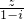为纯虚数，求x的值；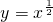
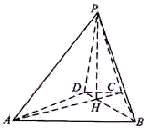如图，已知四棱锥P-ABCD的底面为等腰梯形，AB∥CD，AC⊥BD，垂足为H，PH是四棱锥的高．
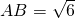，∠APB=∠ADB=60°，求四棱锥P-ABCD的体积．