题目内容
已知函数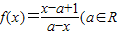 ,且x≠a).
,且x≠a).(Ⅰ) 证明:f(x)+f(2a-x)=-2对函数f(x)在其定义域内的所有x都成立;
(Ⅱ) 当函数f(x)的定义域为
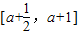 时,求函数f(x)的值域.
时,求函数f(x)的值域.
【答案】分析:(1)计算左边f(x)+f(2a-x)是否等于-2即可;
(2)先化简f(x)=-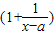 ,只要由求出x-a的取值范围,进而可求出函数f(x)的值域.
,只要由求出x-a的取值范围,进而可求出函数f(x)的值域.
解答:解:(1)证明:当x≠a时,f(x)+f(2a-x)=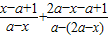 =
=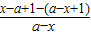 =
=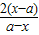 =-2,
=-2,
∴f(x)+f(2a-x)=-2对函数f(x)在其定义域内的所有x都成立;
(2)当x≠a时,f(x)=-1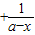 =
=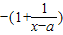 .
.
∵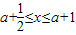 ,∴
,∴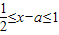 ,∴
,∴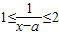 ,∴
,∴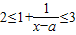 ,
,
∴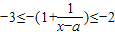 ,即-3≤f(x)≤-2.
,即-3≤f(x)≤-2.
故函数f(x)的值域为[-3,-2].
点评:熟悉证明题的方法和由x的取值求出与之有关的代数式的值是解题的关键.
(2)先化简f(x)=-
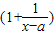 ,只要由求出x-a的取值范围,进而可求出函数f(x)的值域.
,只要由求出x-a的取值范围,进而可求出函数f(x)的值域.解答:解:(1)证明:当x≠a时,f(x)+f(2a-x)=
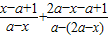 =
=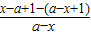 =
=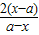 =-2,
=-2,∴f(x)+f(2a-x)=-2对函数f(x)在其定义域内的所有x都成立;
(2)当x≠a时,f(x)=-1
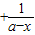 =
=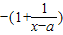 .
.∵
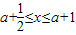 ,∴
,∴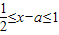 ,∴
,∴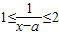 ,∴
,∴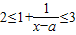 ,
,∴
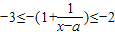 ,即-3≤f(x)≤-2.
,即-3≤f(x)≤-2.故函数f(x)的值域为[-3,-2].
点评:熟悉证明题的方法和由x的取值求出与之有关的代数式的值是解题的关键.

练习册系列答案
 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
 ,且x≠a).
,且x≠a).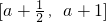 时,求函数f(x)的值域.
时,求函数f(x)的值域.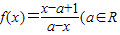 ,且x≠a).
,且x≠a).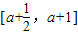 时,求函数f(x)的值域.
时,求函数f(x)的值域.