题目内容
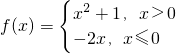，则f（3）+f（-2）的值为
- A.10
- B.12
- C.13
- D.14
D
分析：根据函数的解析式先求出f（3）和f（-2）的值，即可求得f（3）+f（-2）的值．
解答：∵，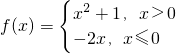
∴f（3）=9+1=10，f（-2）=4，
∴f（3）+f（-2）=10+4=14，
故选D．
点评：本题主要考查利用分段函数求函数的值，体现了分类讨论的数学思想，属于基础题．
分析：根据函数的解析式先求出f（3）和f（-2）的值，即可求得f（3）+f（-2）的值．
解答：∵
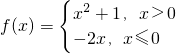，∴f（3）=9+1=10，f（-2）=4，
∴f（3）+f（-2）=10+4=14，
故选D．
点评：本题主要考查利用分段函数求函数的值，体现了分类讨论的数学思想，属于基础题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
偶函数
f(x)在[－4，0]上是减函数，则f(－3)和f(π)的大小关系是[
]|
A ．f(－3)＞f(π) |
B ．f(－3)＜f(π) |
|
C ．f(－3)≥f(π) |
D ．f(－3)≤f(π) |