题目内容
一个圆锥和一个圆柱,下底面在同一平面上,它们有公共的内切球,记圆锥的体积为V1,圆柱的体积为V2,且V1=kV2,则kmin=______.
设球半径为r,圆柱的底面半径也为r,高为2r,
则V2=2πr3.
设圆锥底半径为R=rcotα,高H=Rtan2α.
则V1=
πR2H=
(πr3cos2αtan2α)
则V1:V2=(cos2αtan2α):6.
∵cos2αtan2α=
则当tan2α=
,即tanα=
时,cos2αtan2α取最小值8,
此时kmin=
故答案为:
则V2=2πr3.
设圆锥底半径为R=rcotα,高H=Rtan2α.
则V1=
| 1 |
| 3 |
| 1 |
| 3 |
则V1:V2=(cos2αtan2α):6.
∵cos2αtan2α=
| 2 |
| tan2α-tan4α |
则当tan2α=
| 1 |
| 2 |
| ||
| 2 |
此时kmin=
| 4 |
| 3 |
故答案为:
| 4 |
| 3 |

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
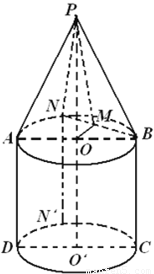
 如图,一个圆锥和一个圆柱组成了一个几何体,其中圆锥和圆柱的底面半径相同,点O,O′,分别是圆柱的上下底面的圆心,AB,CD都为直径,点P,A,B,C,D五点共面,点N是弧AB上的任意一点(点N与A,B不重合),点M为BN的中点,N′是弧CD上一点,且NN'∥AD,PA=AB=BC=2.
如图,一个圆锥和一个圆柱组成了一个几何体,其中圆锥和圆柱的底面半径相同,点O,O′,分别是圆柱的上下底面的圆心,AB,CD都为直径,点P,A,B,C,D五点共面,点N是弧AB上的任意一点(点N与A,B不重合),点M为BN的中点,N′是弧CD上一点,且NN'∥AD,PA=AB=BC=2.
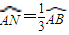 ,求面ANP与面POM所成角的正弦值.
,求面ANP与面POM所成角的正弦值.