题目内容
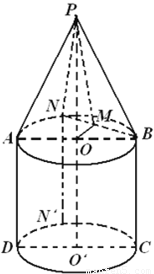
 如图,一个圆锥和一个圆柱组成了一个几何体,其中圆锥和圆柱的底面半径相同,点O,O′,分别是圆柱的上下底面的圆心,AB,CD都为直径,点P,A,B,C,D五点共面,点N是弧AB上的任意一点(点N与A,B不重合),点M为BN的中点,N′是弧CD上一点,且NN'∥AD,PA=AB=BC=2.
如图,一个圆锥和一个圆柱组成了一个几何体,其中圆锥和圆柱的底面半径相同,点O,O′,分别是圆柱的上下底面的圆心,AB,CD都为直径,点P,A,B,C,D五点共面,点N是弧AB上的任意一点(点N与A,B不重合),点M为BN的中点,N′是弧CD上一点,且NN'∥AD,PA=AB=BC=2.(1)求证:BN⊥平面POM;
(2)求证:平面POM∥平面ANN′D;
(3)若点N为弧AB的三等分点且
 |
| AN |
| 1 |
| 3 |
 |
| AB |
分析:(1)证明BN⊥平面POM,连接ON,只需证明BN⊥OM,BN⊥PM,利用线面垂直的判定可证;
(2)连接AN,证明ON∥平面ANN′D,PO∥平面ANN′D,利用面面平行的判定,即可证明平面POM∥平面ANN′D;
(3)过点P作直线l∥OM,取AN中点E,连接PE、EO,可得∠EPO为平面PAN与平面POM所成角,求出PE,OE,即可求得
面ANP与面POM所成角的正弦值.
(2)连接AN,证明ON∥平面ANN′D,PO∥平面ANN′D,利用面面平行的判定,即可证明平面POM∥平面ANN′D;
(3)过点P作直线l∥OM,取AN中点E,连接PE、EO,可得∠EPO为平面PAN与平面POM所成角,求出PE,OE,即可求得
面ANP与面POM所成角的正弦值.
解答:(1)证明:连接ON
∵ON=OB,M为BN的中点,∴△ONB中,BN⊥OM
∵PN=PB,M为BN的中点,∴△PNB中,BN⊥PM
∵OM∩PM=M,
∴BN⊥平面POM;
(2)证明:连接AN
∵O,M分别为AB,BN的中点,∴OM∥AN
∵OM?平面ANN′D,AN?平面ANN′D
∴ON∥平面ANN′D
∵PO∥NN′,PO?平面ANN′D,NN′?平面ANN′D
∴PO∥平面ANN′D
∵OM∩PO=0,
∴平面POM∥平面ANN′D;
(3)解:过点P作直线l∥OM,∵点P在平面POM内,∴l在平面POM内.
又∵AN∥OM,∴直线l∥AN,∴l在平面PAN内.
∴l为平面PAN与平面POM的交线,
取AN中点E,连接PE、EO,
∵PA=PN,∴PE⊥AN,∴PE⊥直线l,
又∵PO⊥OM,∴PO⊥直线l,∴∠EPO为平面PAN与平面POM所成角.
当
=
时,AN=AO=1,
∴直角三角形PAE中,PE=
=
=
,
又△ANO中,OE=
,
∴直角三角形POE中,sin∠EPO=
=
.
∵ON=OB,M为BN的中点,∴△ONB中,BN⊥OM
∵PN=PB,M为BN的中点,∴△PNB中,BN⊥PM
∵OM∩PM=M,
∴BN⊥平面POM;
(2)证明:连接AN
∵O,M分别为AB,BN的中点,∴OM∥AN
∵OM?平面ANN′D,AN?平面ANN′D
∴ON∥平面ANN′D
∵PO∥NN′,PO?平面ANN′D,NN′?平面ANN′D
∴PO∥平面ANN′D
∵OM∩PO=0,
∴平面POM∥平面ANN′D;
(3)解:过点P作直线l∥OM,∵点P在平面POM内,∴l在平面POM内.

又∵AN∥OM,∴直线l∥AN,∴l在平面PAN内.
∴l为平面PAN与平面POM的交线,
取AN中点E,连接PE、EO,
∵PA=PN,∴PE⊥AN,∴PE⊥直线l,
又∵PO⊥OM,∴PO⊥直线l,∴∠EPO为平面PAN与平面POM所成角.
当
 |
| AN |
| 1 |
| 3 |
 |
| AB |
∴直角三角形PAE中,PE=
| PA2-AE2 |
22-(
|
| ||
| 2 |
又△ANO中,OE=
| ||
| 2 |
∴直角三角形POE中,sin∠EPO=
| EO |
| PE |
| ||
| 5 |
点评:本题考查线面垂直,考查面面平行,考查面面角,解题的关键是掌握线面垂直、面面平行的判定,正确作出面面角,属于中档题.

练习册系列答案
 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
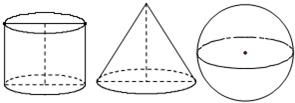 如图,一个圆柱和一个圆锥的底面直径和它们的高都与一个球的直径相等,这时圆柱、圆锥、球的体积之比为
如图,一个圆柱和一个圆锥的底面直径和它们的高都与一个球的直径相等,这时圆柱、圆锥、球的体积之比为

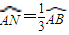 ,求面ANP与面POM所成角的正弦值.
,求面ANP与面POM所成角的正弦值.