题目内容
4个关系式 ①φ⊆{0}②0∈{0}③φ∈{0}④φ={0}其中表述正确的是（ ）
分析：①由空集是任意集合的子集可以判定；
②由元素与集合之间的关系是属于或不属于判定；
③由集合与集合之间是包含关系判定；
④由空集的概念可以判定．
②由元素与集合之间的关系是属于或不属于判定；
③由集合与集合之间是包含关系判定；
④由空集的概念可以判定．
解答：解：①∵φ表示空集，是任意集合的子集，∴φ⊆{0}正确；
②∵0是集合{0}的元素，∴0∈{0}正确；
③∵φ是集合，集合与集合之间是包含关系，∴φ∈{0}不正确；
④∵φ表示空集，集合{0}有一个元素0，∴φ={0}不正确；
综上，其中表述正确的是①②．
故选：A．
②∵0是集合{0}的元素，∴0∈{0}正确；
③∵φ是集合，集合与集合之间是包含关系，∴φ∈{0}不正确；
④∵φ表示空集，集合{0}有一个元素0，∴φ={0}不正确；
综上，其中表述正确的是①②．
故选：A．
点评：本题考查了空集的概念以及元素与集合、集合与集合之间的表述关系，是基础题．
练习册系列答案
相关题目
=
；②|
|=|
|•|
|；③
；④
=
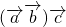；其中正确命题的个数是
｛
｛
∈｛